Logical Scribbles
[최적화] 서포트 벡터 머신(SVM)은 Convex 문제? 본문

다음과 같은 재미있고 엄청난 문제를 생각해보자.

파란색의 동그라미 종족과 빨간색의 세모 종족은 서로 사이가 매우 나쁘다. 만약 그들이 함께 산다면 대참사가 일어난다고 가정해보자. 따라서 우리는 그들의 국경을 그어야 하는 상황이다. 우선 그냥 내 마음대로 국경을 그어보겠다.

너무 비인간적으로 국경을 그린 것 같다. 왜냐하면, 국경에 가장 가까운 동그라미와 세모가 가까워도 너무 가깝기 때문이다. 다시 그리자.

국경을 다시 그려봤다. 하지만 빨간색 세모 종족의 반발이 엄청날 것이다. 왜냐햐면 그들의 땅의 면적이 줄었기 때문이다.
그렇다면 두 종족이 모두 만족할 수 있는 국경은 어떻게 그어야할까? 답은 간단하다.

국경에서 가장 가까운 종족까지의 거리가 가장 멀도록 설정하면 되는 것이다. 직관적으로는 간단하지만 수학적으로는 상당히 복잡한 문제이다.
이렇듯 두 부류 사이의 여백(margin)이 가장 넓어지면(둘이 가장 떨어져 있으면(=margin최대화)) 그 둘을 가장 잘 분류했다고 할 수 있다.
서포트 벡터 머신(SVM)이란 위 예시와 같은 두 클래스로부터 가장 멀리 떨어져있는 결정 경계를 찾는 분류기이고, 패턴인식에서 높은 정확도를 보이는 기법이다.
따라서 우리의 목적은 두 클래스를 가장 잘 구분할 수 있는 Hyper Plane(이 예시에서는 직선의 방정식)을 찾는 것이다.
이를 수학적으로 살펴보도록 하자.

ax+by=c라는 직선의 방정식은 [a,b] 벡터와 [x,y]^T 벡터의 내적 값이 c가 된다는 것과 동치이다. 이 때 [a,b] 벡터를 w라는 notation을 이용하여 표현하고 [x,y]^T 벡터를 d라는 notation을 이용하여 표현 하면, 직선은 w^T*d = c 와 같이 표현할 수 있다.
이는 벡터의 내적이기 때문에 w와 d의 2 Norm 을 각각 곱하고 벡터 사이의 각도의 코사인 값을 곱했을 때, c가 결과값으로 나오는 식과 동일하다는 것을 알 수 있다.
그리고 이를 기하학적으로 생각했을 때, w 벡터에 대해 내적이 취해졌을 때 항상 c라는 값을 도출해내는 벡터 d의 자취는 직선이 됨을 알 수 있다. 그리고 w벡터의 시점에서 직선까지의 거리는 다음과 같이 표현된다.


이제 파란색 동그라미 종족과 빨간색 세모 종족에 직선을 하나씩 그리자. 그러면 위의 그림과 같이 w^T*d = c+1 , w^T*d = c-1로 표현할 수 있다. (c+1, c-1 로 설정할 수 있는 이유는 직선의 방정식에서 a,b값을 적절히 조절하면 되기 때문이다.)
그렇다면 이제 위의 주황색 직선 두개의 거리 M은 다음과 같음을 알 수 있다.
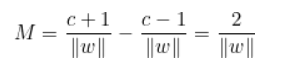
앞서 국경을 선택할 때는 이 거리가 가장 커져야 한다고 언급했었다. 즉 위의 거리 값을 maximize할 수 있는 w를 선택해야 한다는 것이다. 따라서 우리의 문제는 다음과 같아진다.

이제 국경 선택의 문제가 수학적으로 정의 되었다. 잘 생각해보면 SVM문제는 convex optimization problem임을 알 수 있을 것이다. 그런데 문제가 하나 있다.
위의 M만 최대화 하면 끝일까? 아니다!
우리에게는 제약조건이 있다. 바로 동그라미 부족과 세모 부족이 그들만의 나라를 가져야 한다는 것이다. 만약 국경이 아래와 같이 그려진다면 M은 매우 크겠지만, 동그라미 부족과 세모 부족이 함께 살아야하는 대참사가 일어날 수 있다. 따라서 다음과 같은 조건도 필수적이다.

그런데 위 식은 추가적인 함수 S를 통해 하나로 통합될 수 있다. S 함수가 의미하는 것은 만약 포인트가 동그라미 부족이면 1이고, 세모 부족이면 -1이라는 것이다.
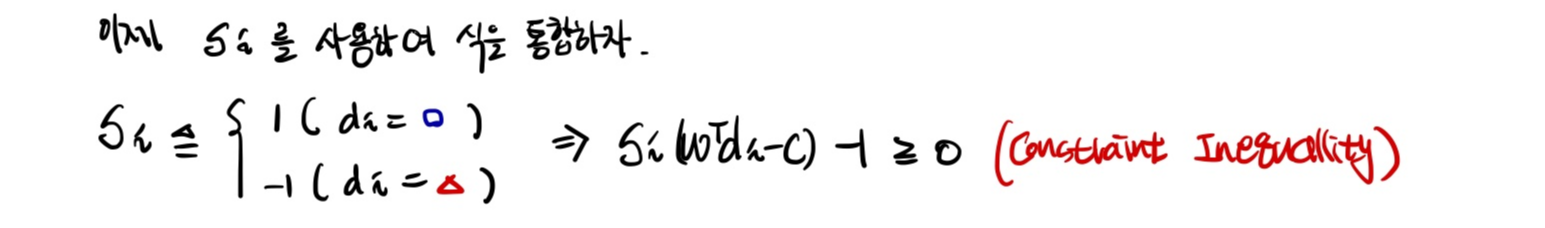
이제 모든 준비가 끝났다. 지금까지 수학적으로 정의한 SVM 문제를 다시 정리해보자.

혹은 (notation들이 바뀌니 잘 따라와야한다)

위의 우리의 문제를 보면 정확히 primal optimization problem임을 알 수 있다.

만약 제약조건이 등호라면 라그랑주 승수법으로 해결하면 되지만, 우리의 문제는 부등식 제약조건을 갖고 있다. 따라서 이 역시 Lagrangian으로 풀어나갈 것이지만, 특별한 조건이 만족되어야 한다. 바로 KKT 조건이다!
문제의 최적해 x스타에 대해 다음 명제를 모두 만족시키는(KKT 조건을 성립시키는) 가 존재한다.

위 조건을 우리의 국경 문제로 바꾸면 다음과 같은 KKT조건이 충족되어야 한다.

이 때 우리는 αi > 0 일때만 신경을 써줄 것이다. 우선 기하학적으로 생각했을 때 αi =0 임은 아무 의미가 없기 때문이다.

그 이유는 위의 그림에서 판단할 수 있는데, 만약에 α = 0이면 g(x) 제약조건이 아무 의미가 없어져 버리고 오직 f(x)의 최적화 문제로 변하기 때문이다.
그러면 이제 Lagrangian을 적용해보자.

이제 KKT 조건에서 stationary를 이용하면 , 다음을 얻을 수 있다.

따라서 이를 정리하면 아래 식을 얻는다.

이쯤에서 변수를 정리해보자. 최적의 w를 얻기 위해서는 α,t,x가 필요한데 이제 우리에게 남은 변수는 α뿐이다. α를 알기위해서는 위의 식을 다시 lagrangian 식에 대입해준다.
그러면 lagrangian의 첫번째 항은 아래와 같은 식을 통해 α로만 이루어진 식이되고,

두번째 항도 마찬가지로 α로만 이루어진 식이된다. 아래식에서 0이 되는 항이 존재하는데, 그 이유는 위의 stationary condition 때문이다.

이제 둘을 합쳐주면

위 식이 나오게 된다.
이제 이 문제를 Dual 문제로 바꾸어 풀어야 한다. 다음을 이용해야 한다.


위의 g스타는 dual의 최적값이다.
우리의 문제는 Objective function이 convex이고 inequality constraint가 affine이므로 slater 조건을 만족한다.
따라서 우리의 문제는 strong duality가 성립하고, 아래의 결과가 나온다.

따라서 우리의 문제를 dual problem으로 바꾸어 풀 수 있음이 보여졌고, dual problem은 다음과 같다.

이를 우리의 문제로 바꾸어 표현하면,

이제 위 문제는 컴퓨터에게 맡기자.
컴퓨터는 α를 리턴할 것이고, 이를 통해 w와 b를 알 수 있다. 어떻게?
w는 아래의 식에서 구하고,

b는 아래의 식에서 구한다. 앞서 α가 0이되면 의미가 없기 때문에 α를 양수 취급함을 이용하여 좌변의 두번째 항만 0이면 됨을 이용한다.

이렇게 해서 support vector가 여러개가 나오는데, b의 값을 평균내어 결정해주면 드디어 우리의 국경을 구할 수 있게 된 것이다.
끝!
'딥러닝 > 딥러닝 이론' 카테고리의 다른 글
| [객체 인식] Selective Search란? (Selective search for object recognition. IJCV, 2013) (0) | 2023.11.20 |
|---|---|
| [객체 탐지] Hard Negative Mining 이란? (0) | 2023.11.20 |
| [객체 탐지] 2-Stage Dectector 와 1-Stage Detector (0) | 2023.11.18 |
| [최적화] Basic Inequality의 증명 (0) | 2023.11.15 |
| [객체 탐지] HOG(Histogram of Oriented Gradient for human detecting)에 대하여 (1) | 2023.11.14 |




