Logical Scribbles
[객체 탐지] HOG(Histogram of Oriented Gradient for human detecting)에 대하여 본문
[객체 탐지] HOG(Histogram of Oriented Gradient for human detecting)에 대하여
KimJake 2023. 11. 14. 21:34
이번 포스팅에서는 'Histogram of Oriented Gradient for human detecting' 라고도 불리는 HOG에 대해 알아보자. 내가 HOG를 공부하게 된 계기는 R-CNN 논문을 읽다가 제일 처음 막혔던 부분이었기 때문이다. R-CNN 논문에서 그 때 당시의 문제점으로 HOG 방식이 정체되고 있다는 말이 나오는데, HOG 방식이 대체 뭔가하고 알아보았다.
우선 Histogram of Oriented Gradient for human detecting을 직역해보자. '인간 탐지를 위한 기울기 기반의 히스토그램' 아직은 무슨말인지 잘 이해가 되지 않는다.
먼저 GPT한테 물어보았다.

대충 감이 잡힌다. 처음에는 이미지의 픽셀에 대해 그래디언트를 계산한 후 셀 내에서 이의 방향과 크기를 히스토그램으로 만들고, 더 큰영역 '블록'에서 히스토그램을 정규화 하고 이를 이어붙이는 방식이구나~ 라고 이해했다. 히스토그램은 알겠는데 그렇다면 이미지의 그래디언트와 셀은 무엇이고, 블록은 무엇인가?
1. 이미지의 그래디언트
이름에서도 느껴지듯 이미지의 그래디언트는 HOG방식의 키포인트다. 먼저 이미지의 그래디언트에 대해 알아보자.
그래디언트는 공대생 혹은 자연대생이면 많이 들어보았을 용어이다. 여기서는 더 단순히 생각해도 될 듯 하다.

그래디언트는 단순하게 말하면 기울기이다. 즉 y변화량을 x변화량으로 나눈 값이다. 이 그래디언트의 개념을 이미지에 적용시켜 보자.
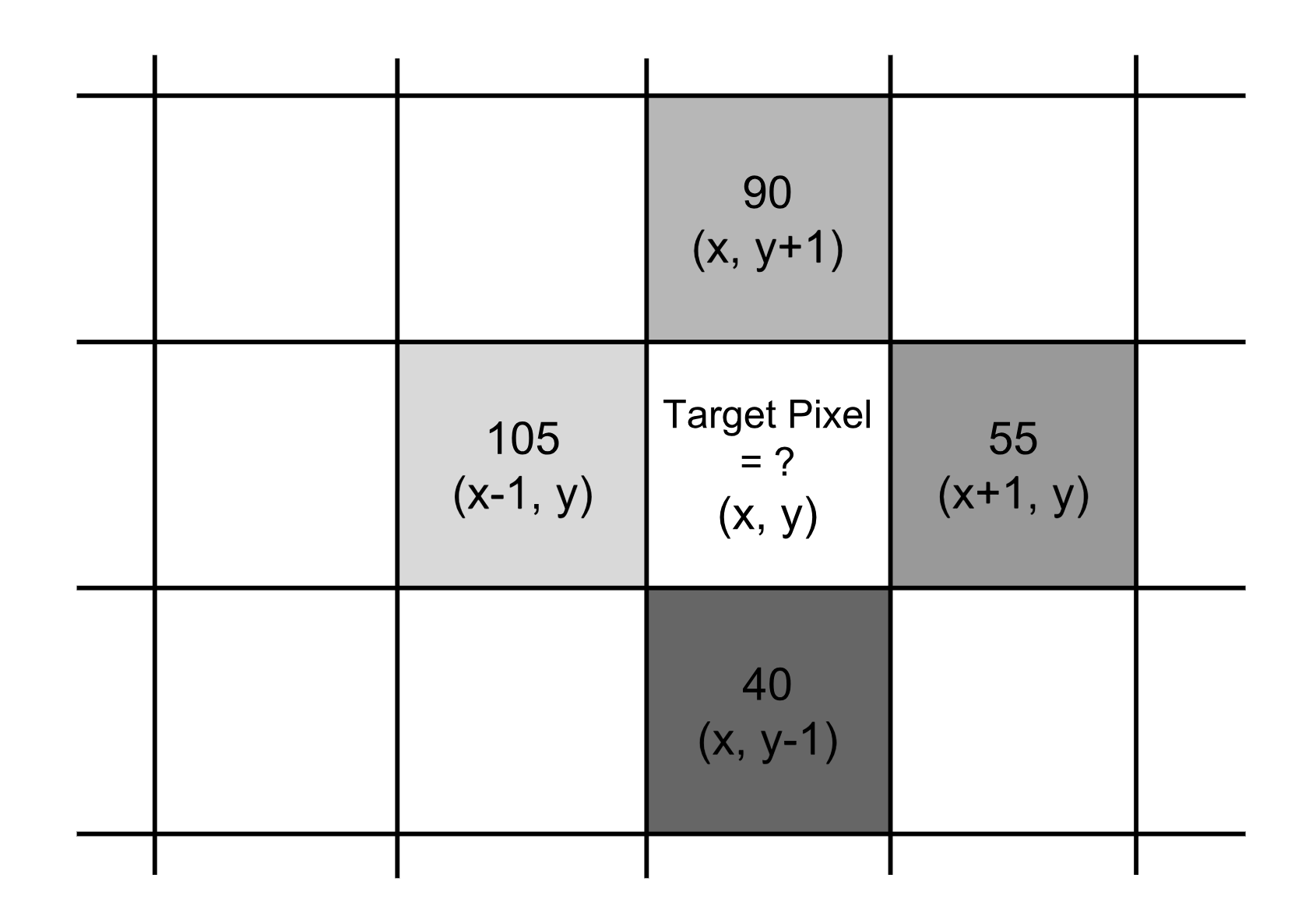
위 사진을 보면, 2행 3열에 우리의 타겟 픽셀이 있다. 저 타겟 픽셀에 대하여 그래디언트를 계산하고 싶다.
타겟 픽셀의 오른쪽과 왼쪽 픽셀에 대해, 픽셀에 적힌 숫자의 차이는 -50이다. 또한 타겟 픽셀의 위쪽과 아래쪽 픽셀에 대해 픽셀에 적힌 숫자의 차이는 50이다.
x축 방향 기울기 변화량, y축 방향 기울기 변화량을 함께 표현한 값을 기울기 벡터(gradient vector)라고 하기로 약속하자. 그러면 타겟 픽셀을 기준으로 기울기 벡터는 이렇게 된다.

벡터는 방향과 크기를 갖는 물리량이라고 공부했던 기억이 있다면, 자연스럽게 벡터의 크기와 방향은 어떻게 구하는지 궁금해진다. 벡터의 크기는 {50^2 + (-50)^2}^(1/2) = 70.7107 이 되고, 벡터의 방향은 arctan(-50/50) = -45도가 된다.
이 벡터를 표현하면 다음과 같다.

2. 픽셀, 셀, 블록
픽셀은 말그대로 이미지의 한 픽셀 단위이다. 이를 여러개 묶으면 셀이 되고, 셀을 여러개 묶으면 블록이 된다. 즉 블록은 셀을 포함하는 개념이고, 셀은 픽셀을 포함하는 개념이다.
보행자 검출을 위한 영상으로는 보통 64*128의 사이즈를 이용하고, 보통 8*8을 한 셀로 정한다고 한다. (물론 셀의 크기는 다르게 정해도 된다.)
3. 이미지의 그래디언트를 이용한 히스토그램

히스토그램이란 기본적으로 x축에 계급을, y축에 도수를 표현하는 그래프이다. 이미지의 그래디언트를 이용한 히스토그램에서 계급은 그래디언트 방향의 크기로 정한다. 0도 ~ 180도를 20도씩 자르면 총 9개의 계급이 나오고, 각각의 계급마다 도수를 써준다. 위의 예시에서 -45도가 그래디언트의 방향이었는데, 그렇다면 -45도는 어떤 계급에 넣어야 할까?
경험적으로 보행자 인식에서 그래디언트의 부호를 무시하고 HOG를 진행하였을 때, 객체 인식이 더 잘된다는 것을 알게 되었다. 따라서 -45도와 45도를 같게 취급하여 알맞는 계급에 넣는다.
y축에 해당하는 도수로는, 벡터의 크기를 누적시켜 구해준다. 위 그림의 빨간색 픽셀과 같이 만약 어떤 표본이 계급의 중앙값에 위치한다면, 반반을 나눠 각각 누적 시켜준다.
우리는 1개의 이미지에 대해 이미지의 다양한 영역에서 이러한 히스토그램을 만들고, 어떤 부분에서 어떤 특징이 있는지 파악하길 원한다. 따라서 HOG는 히스토그램을 셀 단위로 구하여 이미지의 특징을 파악한다.
비슷한 이미지는 서로 비슷한 히스토그램을 그릴 것이다. 또한, 보통 물체의 테두리(edge) 부분은 그래디언트가 클 것이다. 왜냐하면, 우리가 물체의 테두리를 '물체의 테두리 부분에서 눈에 들어오는 빛의 밝기 차이'로 인식하기 때문이다.

이렇게 방향을 계급으로 갖고 누적 크기를 도수로 갖는 이미지의 그래디언트를 이용한 히스토그램의 엄청난 장점은 edge에서의 gradient가 얼마나 큰지에 대한, 그리고 그 그래디언트의 방향를 구분하는 feature 을 가지고 있다는 것이다. 픽셀 한개에 대해 히스토그램을 구하는 것이 아닌 셀 단위로 벡터의 누적 크기를 구하여 만들어지기 때문에 HOG를 이용한 모델 자체가 견고하고, 노이즈에도 강하다.
이렇게 구해진 셀마다의 히스토그램을 이제 블럭 관점으로 확대시킬 것이다. 앞서 말했듯이 블럭은 여러 셀이 모인 단위이다.

예를 들어 1개의 블록에 4개의 셀이 들어간다고 하면, 위의 그림과 같은 상황이 될 것이다.
블록의 각 셀(4개)에 대해 히스토그램을 연결한 다음, 전체 feature vector를 정규화하는 L1, L2를 이용한다.

앞서 말했듯 테두리 값의 그래디언트는 주변 밝기에 영향을 많이 받는다. 이에 대한 민감성을 없애주려고 정규화를 한다고 한다. (가장 이상적인 상황은 어떠한 조명에도 완벽하게 객체를 탐지하는 것이기 때문이라고 이해했다) 정규화는 블록 단위로 진행이 되는데, 각 블록은 전체 이미지를 순회하면서 정규화를 한다. 이때 겹치는 부분이 발생하는데 이 부분을 블록 스트라이드(blcok stride)라고 한다.
이제 예를 통해 이 개념들을 이해해 보자.
64*128 픽셀의 이미지에서 16*16 픽셀이 블록을 이루고, 8*8 픽셀이 셀을 이룬다고 가정해보자.(보통 블록의 크기는 셀의 크기의 2배로 정한다고 한다.) 16*16의 블록을 통해 합쳐진 히스토그램은 총 36개의 계급이 있을 것이다.(9*4=36) 블록이 8픽셀 단위로 이동한다 했을 때 이 히스토그램이 정규화 되면, 정규화를 계산하는 횟수는 7 x 15= 105번이다. ({64/(16-8) - 1} x {128/(16-8) - 1} = 105, 8은 블록 스트라이드) 따라서 전체 그래디언트의 개수는 36*105 = 3780이 된다.
이제 전체의 이미지에 대한 전체 그래디언트를 구할 수 있게 되었다. 이제 이걸로 어떡하란 말인가..?
이 전체적인 그래디언트의 학습을 위해 머신러닝에서 많이 나오는 SVM을 이용한다. 이 부분은 나도 잘 이해가 되지 않아 지금까지 이해한 것을 적어보면, 위에서 계산된 그래디언트로 이루어진 이미지(feature vector)와 label로 이루어진 쌍이 선형 SVM 분류기를 통해 학습되어 Test 시에도 효과적으로 해당 이미지를 찾아낼 수 있도록 하는 것 같다.
다음 시간에는 이 HOG를 이용하여 객체인식을 하는 코드를 직접 구현해보도록 하겠다.
끝!
'딥러닝 > 딥러닝 이론' 카테고리의 다른 글
| [최적화] 서포트 벡터 머신(SVM)은 Convex 문제? (0) | 2023.11.18 |
|---|---|
| [객체 탐지] 2-Stage Dectector 와 1-Stage Detector (0) | 2023.11.18 |
| [최적화] Basic Inequality의 증명 (0) | 2023.11.15 |
| [객체 탐지] IoU(Intersection over Union), mAP(Mean Average Precision)이란? (0) | 2023.11.13 |
| [딥러닝] Batch-Nomalization(배치 정규화)의 기초적 이해 (0) | 2023.10.29 |




