Logical Scribbles
[선형대수학] PCA(주성분 분석)을 이용한 얼굴 인식 (Python) 본문
이번 포스팅에서는 PCA(주성분 분석)을 이용하여 Python에서 얼굴 인식을 진행해보자. PCA에 대한 글은 곧 올릴 예정이다.
크게 두가지 알고리즘으로 성능 평가를 해볼 것이다.
- k-NN 알고리즘
- SVM
데이터는 sklearn에서 제공하는 'fetch_lfw_people'이라는 데이터셋을 사용할 것이다.
sklearn.datasets.fetch_lfw_people
Examples using sklearn.datasets.fetch_lfw_people: Faces recognition example using eigenfaces and SVMs
scikit-learn.org
데이터셋의 구성은 다음과 같다.

먼저 필요한 모듈들과 데이터셋을 다운 받아오자.
from google.colab import drive
drive.mount('PCAforFun')
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import seaborn as sns
from sklearn.svm import SVC
# Load the LFW dataset
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
fetch_lfw_people에는 많은 parameter들을 입력할 수 있는데 나는 한 사람당 최소 이미지 개수와 resize를 넣어주었다.
이제 데이터를 확인해보자.
lfw_people
#output
{'data': array([[0.9973857 , 0.99607843, 0.9921568 , ..., 0.38169935, 0.38823533,
0.3803922 ],
[0.14771242, 0.19738562, 0.1751634 , ..., 0.45751634, 0.44444445,
0.53594774],
[0.34379086, 0.39477125, 0.49150327, ..., 0.709804 , 0.72156864,
0.7163399 ],
...,
dtype=float32),
'images': array([[[0.9973857 , 0.99607843, 0.9921568 , ..., 0.29803923,
0.24836601, 0.20653595],
[0.9973857 , 0.9921569 , 0.9908497 , ..., 0.30588236,
0.2535948 , 0.21568628],
[0.96078426, 0.93071896, 0.8679738 , ..., 0.2875817 ,
0.24183007, 0.21568628],
...,
[0.34509805, 0.26143792, 0.17385621, ..., 0.4248366 ,
0.40261438, 0.39084968],
[0.30980393, 0.23398693, 0.17124183, ..., 0.39869282,
0.4013072 , 0.3764706 ],
[0.28366014, 0.2248366 , 0.18039216, ..., 0.38169935,
0.38823533, 0.3803922 ]],
...,
[0.18169935, 0.17254902, 0.17254902, ..., 0.09281046,
0.07058824, 0.13986929],
[0.16470589, 0.1633987 , 0.1764706 , ..., 0.0875817 ,
0.10326798, 0.1764706 ],
[0.17908497, 0.19477125, 0.20392157, ..., 0.13333334,
0.13725491, 0.2535948 ]]], dtype=float32),
'target': array([5, 6, 3, ..., 5, 3, 5]),
'target_names': array(['Ariel Sharon', 'Colin Powell', 'Donald Rumsfeld', 'George W Bush',
'Gerhard Schroeder', 'Hugo Chavez', 'Tony Blair'], dtype='<U17'),
아래의 사진을 참고하여 각 column이 의미하는 아웃풋을 확인할 수 있다. (아웃풋이 너무 길어 일부분만 가져왔다.) 'data'와 'images'의 차이를 잘 파악해두어야 할 것 같다.

이제 궁금한 것들도 마저 확인해보자.
print(len(lfw_people.data))
print(len(lfw_people.images))
print((lfw_people.target_names))
# 1288
# 1288
# ['Ariel Sharon' 'Colin Powell' 'Donald Rumsfeld' 'George W Bush'
# 'Gerhard Schroeder' 'Hugo Chavez' 'Tony Blair']
내가 입력한 parameter에 대해 데이터와 이미지는 1288개, 그리고 사람은 7명정도가 리턴되었다.
이제 이미지 1개를 가져와 shape과 이미지를 직접 확인해보자.
tt = lfw_people['images'][2]
tt.shape
plt.imshow(tt)
plt.show()
#(50*37)
이제 본격적으로 얼굴 인식을 수행해보자!
0. 데이터셋 준비하고 전처리 하기
X = lfw_people.data
n_samples, n_features = X.shape
y = lfw_people.target
# 데이터를 나누자
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 데이터 전처리(스케일링)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 데이터의 평균을 계산하여 모든 데이터들을 원점 주변으로 모아주자
mean = np.mean(X_train, axis=0)
# 원점 주변으로 이동
X_centered = X_train - mean
1. 공분산 행렬을 만들자.
# 공분산 행렬 계산하기
cov_matrix = np.cov(X_centered, rowvar=False)
print(cov_matrix)
print("-------------------------------------------------------------------")
print(cov_matrix.T)

나는 약간 의심병이 생겨 다시 한번 확인해 보았다.
# 공분산 행렬이 대칭행렬인지 확인해보자.
np.array_equal(cov_matrix, cov_matrix.T, equal_nan=False)
True
2. 공분산 행렬의 고유값과 고유벡터를 찾아주자. (고유값 분해)
# 이제 공분산 행렬의 고유값과 고유벡터를 구해보자
eigenvalues, eigenvectors = np.linalg.eigh(cov_matrix)
print(eigenvalues)
print("num of eigenvalues :",len(eigenvalues))
print("-------------------------------------------------------------------")
print(eigenvectors)
print("num of eigenvectors :",len(eigenvectors))

예상대로 1850개의 고유값과 고유벡터가 리턴되었다.
3. 고유벡터를 고유값의 크기에 따라 정렬하자.
# 고유벡터를 정렬하자
sorted_indices = np.argsort(eigenvalues)[::-1]
eigenvectors_sorted = eigenvectors[:, sorted_indices]
4. 차원 축소하기
# PCA를 위한 주성분 개수를 고르자
n_components = 150 # 1850차원을 150차원으로 축소
# 개수만큼 고유벡터 선택
reduced_eigenvectors = eigenvectors_sorted[:, :n_components]
# 내적될 행렬의 shape를 확인
print(X_centered.shape)
print(reduced_eigenvectors.shape)
#(1030, 1850)
#(1850, 150) 결과값으로 1030 x 150 의 행렬이 나올 것임!
# 데이터를 내적
X_train_pca = np.dot(X_centered, reduced_eigenvectors)
X_test_pca = np.dot(X_test - mean, reduced_eigenvectors)
print(X_train.shape)
# output = (1030,1850)
print(X_train_pca.shape)
# output = (1030,150) 차원이 축소됨을 확인할 수 있다.
5. 성능 평가하기
1) KNN
# KNN 알고리즘으로 성능평가를 해보자.
def k_nearest_neighbors(X_train, y_train, X_test, k=5):
n_test = X_test.shape[0]
y_pred = np.zeros(n_test, dtype=int)
for i in range(n_test):
# 거리 계산
distances = np.linalg.norm(X_train - X_test[i], axis=1)
# 가장 가까운 데이터의 index
nearest_indices = np.argsort(distances)[:k]
# label 얻기
nearest_labels = y_train[nearest_indices]
unique, counts = np.unique(nearest_labels, return_counts=True)
y_pred[i] = unique[np.argmax(counts)]
return y_pred
# k 값 정하기
k = 5
#함수 실행
y_pred_knn_pca = k_nearest_neighbors(X_train_pca, y_train, X_test_pca, k)
# 평가
accuracy_knn_pca = accuracy_score(y_test, y_pred_knn_pca)
print(f"k-NN with PCA Accuracy: {accuracy_knn_pca:.4f}")
#k-NN with PCA Accuracy: 0.6008
2) SVM
# SVM이용하기
clf_svm_pca = SVC(C=1.0, kernel='rbf', gamma='scale', class_weight='balanced', random_state=0)
clf_svm_pca.fit(X_train_pca, y_train)
y_pred_svm_pca = clf_svm_pca.predict(X_test_pca)
# 평가하기
accuracy_svm_pca = accuracy_score(y_test, y_pred_svm_pca)
print(f"SVM with PCA Accuracy: {accuracy_svm_pca:.4f}")
#SVM with PCA Accuracy: 0.7907
SVM이 성능이 더 좋은 것을 확인할 수 있다.
이제 classification_report, confusion_matrix를 통해 둘을 비교해보자.
# KNN
report_knn_pca = classification_report(y_test, y_pred_knn_pca, target_names=lfw_people.target_names)
print("k-NN with PCA Classification Report:\n", report_knn_pca)
conf_matrix_knn_pca = confusion_matrix(y_test, y_pred_knn_pca)
plt.figure(figsize=(10, 8))
sns.heatmap(conf_matrix_knn_pca, annot=True, fmt="d", cmap="Blues", xticklabels=lfw_people.target_names, yticklabels=lfw_people.target_names)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('k-NN with PCA Confusion Matrix')
plt.show()
# SVM
report_svm_pca = classification_report(y_test, y_pred_svm_pca, target_names=lfw_people.target_names)
print("SVM with PCA Classification Report:\n", report_svm_pca)
conf_matrix_svm_pca = confusion_matrix(y_test, y_pred_svm_pca)
plt.figure(figsize=(10, 8))
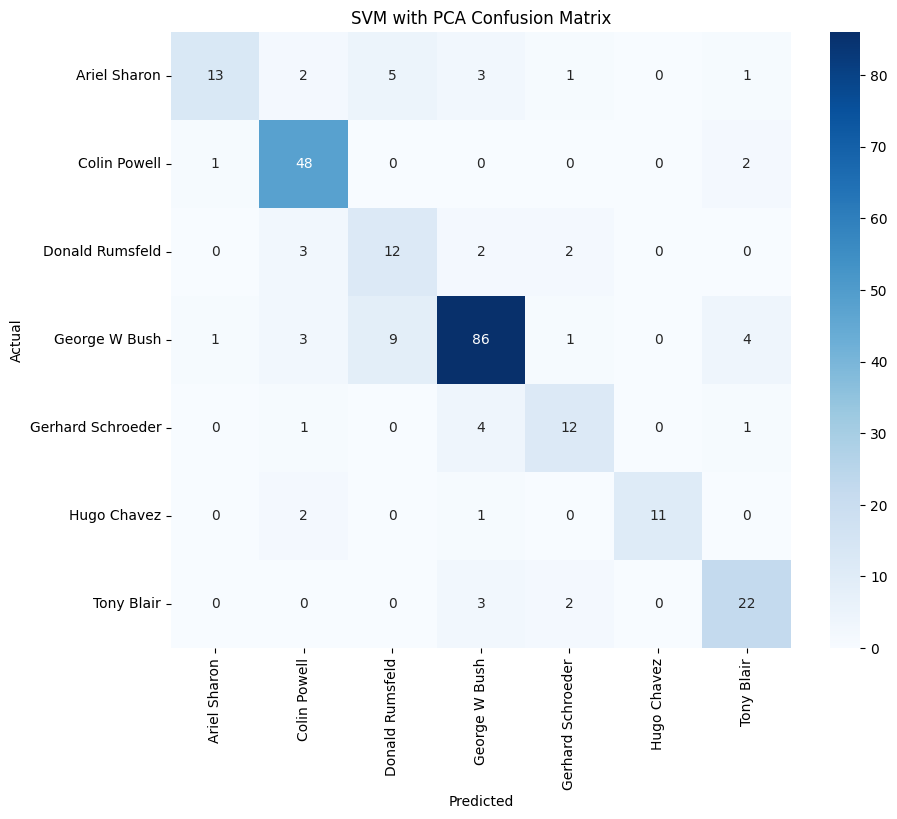
sns.heatmap(conf_matrix_svm_pca, annot=True, fmt="d", cmap="Blues", xticklabels=lfw_people.target_names, yticklabels=lfw_people.target_names)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('SVM with PCA Confusion Matrix')
plt.show()



끝!
'기초 수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] PCA(주성분 분석)란? (0) | 2023.11.23 |
|---|---|
| [선형대수학] 특이값 분해(SVD)의 응용 (0) | 2023.11.21 |
| [선형대수학] 특이값 분해(SVD) (0) | 2023.11.21 |
| [선형대수학] 고유값 분해 (0) | 2023.11.19 |
| [선형대수학] 고유값(Eigenvalue)과 고유벡터(Eigenvector) (0) | 2023.11.18 |




