[논문 리뷰] Attention Is All You Need (Transformer)

오늘은 대망의 'Attention Is All You Need' 논문에 대해서 리뷰해보겠다.
 

Attention Is All You Need

 
사실 최근의 몇몇 포스팅들이 이 리뷰를 위한 빌드업이었다. 우선 기초 지식을 위해 아래의 내용을 숙지하고 읽는 것을 추천한다. 추가적으로 선형대수학에 대한 지식이 있어야 읽기 수월하다.
 

[딥러닝] 원-핫 인코딩과 워드 임베딩

 
 

[딥러닝] 어텐션 메커니즘(Attention Mechanism)이란?

 
 

[딥러닝] RNN(Recurrent Neural Network)이란?

 

[딥러닝] Seq2Seq 와 거자일소(去者日疎 )

 

이제 시작해보자.

 
1. 기존 방식의 문제점 그리고 해결

 
기존 방식의 문제점은 위 포스팅들에서 너무나도 많이 소개가 되었다. 기존의 자연어 처리 분야에서는 RNN 구조가 널리 사용되고 있었으나, RNN은 고질적인 long-term depency 문제가 존재하였다. 따라서 어텐션 메커니즘이 그 대안으로 등장하였는데, 어텐션 메커니즘을 사용하더라도 RNN 기반의  Seq2Seq 모델에 적용되어 위의 단점들을 보완하는데 그쳤다.
 
하지만 본 논문은 RNN 구조를 완전히 버리며 어텐션 메커니즘만을 사용한 시퀀스 데이터 처리 방법을 고안하였고,(따라서 논문 제목이 아주 자극적이다.) 이 논문을 통해 어텐션 메커니즘이 Seq2Seq 모델을 완벽하게 대체할 수 있게 되었다. 논문에서 제시한 모델은 RNN을 사용하지 않고 인코더-디코더 구조를 설계하였음에도 성능적인 측면에서 RNN 기반 모델보다 우수한 성능을 보여주었다. (병렬 처리 및 계산 복잡도와 관한 내용을 뒤에서 다룰 것이다.) 이 모델을 트랜스포머(Transformer)라고 이름 붙였다.
 

2. 트랜스포머(Transformer)의 구조

트랜스포머 모델 구조

 
이때 당시 SOTA를 달성했던 모델들은 인코더-디코더 구조를 적극적으로 채택하고 있었다. 위의 글들에도 정리가 되어 있지만, 간략하게 인코더-디코더 구조를 살펴보자. 

1. 인코더에 인풋 시퀀스 데이터 X가 입력된다.
2. 인코더 내부에서 X와 매핑되는 hidden state Z가 만들어진다.
3. Z는 디코더의 인풋 데이터로 입력된다.
4. 디코더 내부에서 Z와 아웃풋 시퀀스 데이터 Y를 매핑하여 출력한다.

트랜스포머도 이러한 인코더-디코더 구조를 채택하였다. 하지만 트랜스포머가 기존의 모델과 다른 점은 RNN이나 convolution 시퀀스 모델을 사용하지 않고 입력과 출력의 표현을 계산하기 위해 전적으로 self-attention에 의존한다는 것이다. 
 
이제부터는 트랜스포머의 구조를 하나 하나씩 뜯어서 살펴보자.
 

2-1. 인코더-디코더
 

인코더 : 인코더는 6개의 동일한 레이어로 구성되어 있다. 각각의 레이어는 두개의 서브 레이어를 갖는데, 첫번째 레이어는 multi-head attention 레이어이고, 두번째는 feed forward network이다. 이들은 두 서브 레이어에 RseNet의 잔차 연결을 이용한 뒤, layer nomalization을 적용하였다. (위의 그림을 보면 이해하기 더 쉬울 것이다.) 따라서 한개의 서브 레이어를 통과한 결과는 아래와 같을 것이다.

 
임베딩 레이어를 포함한 모든 서브 레이어는 d_model = 512 차원의 아웃풋을 출력한다.
 
디코더 : 디코더도 6개의 레이어로 구성되어 있다. 인코더와 달리 디코더는 1개의 추가적인 서브 레이어를 갖는다. 이 서브 레이어는 인코더의 아웃풋을 키와 벨류로 받아 multi-head attetion을 수행하는 역할을 한다. 디코더에서도 잔차 연결 이후 layer nomalization을 수행한다. 디코더가 인코더와 다른 또다른 중요한 점은 masking이 적용되었다는 것이다.
 
masking 이란?
 
트랜스포머는 seq2seq와 마찬가지로 교사 강요(Teacher Forcing) 을 사용하여 훈련한다.
 

Teacher forcing - Wikipedia

 
간단하게 말하면 훈련 과정에서 정답지로 훈련을 시키는 것인데, 트랜스포머의 구조 특성상 학습 과정에서 번역할 문장에 해당되는 행렬을 한 번에 입력 받는다. 이 문장 행렬을 한 번에 입력 받는 방식에서 문제가 발생한다.
 
트랜스포머는 문장 행렬로 입력을 한 번에 받으므로 현재 시점의 단어를 예측하고자 할 때, 정답지의 미래 시점의 단어까지도 참고할 수 있는 현상이 발생한다. 이를 방지하기 위해 트랜스포머의 디코더에서는 현재 시점의 예측에서 미래 시점의 단어들을 참고하지 못하도록 룩-어헤드 마스크(look-ahead mask)를 도입하였다. 이를 masking 기법이라 한다.
 

masking 기법

  
6개의 층을 쌓았기 때문에 전체적인 구조는 아래와 같다.

2-2.Self-attention
 

self-attention이란 말그대로 어텐션 메커니즘을 자기 자신에게 수행한다는 의미를 담고 있다. 어텐션 메커니즘을 리마인드 해보자. 

Attention Mechanism

 
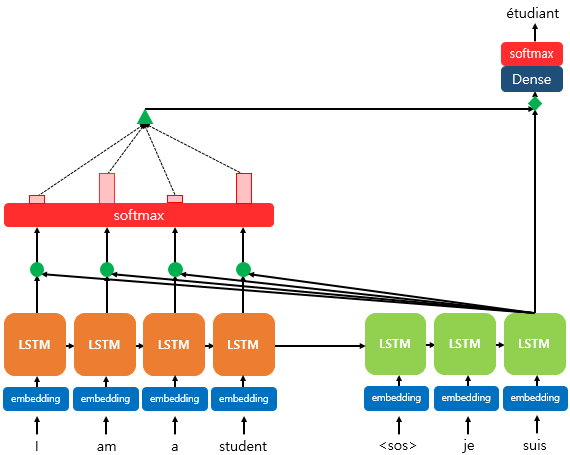
위 어텐션 메커니즘에서 쿼리, 키, 값을 기억해보자.

• 쿼리(Query) : t 시점의 디코더 셀에서의 은닉 상태 -> 현재 출력 단어를 나타내는 벡터
• 키(Key) : 모든 시점의 인코더 셀의 은닉 상태들 -> 입력 시퀀스의 벡터들
• 벨류(Value) : 모든 시점의 인코더 셀의 은닉 상태들 -> 입력 시퀀스의 벡터들

 이 때의 핵심은 key, value는 입력 시퀀스의 벡터들이고 query는 디코더 셀에서의 은닉 상태라는 것이다. 
 
self attention은, 이 쿼리와 키와 벨류값을 모두 입력 시퀀스의 벡터들로 선택한다. 따라서 어텐션 메커니즘을 자기 자신에게 취하는 형태가 될 수 있는 것이다. (자기 자신을 참조한다고 생각하면 될 것 같다.) 이러한 self-attention에서 쿼리, 키와 벨류값을 정리해보면 다음과 같을 것이다.

• 쿼리(Query) : 입력 문장의 모든 단어 벡터들
• 키(Key) :  입력 문장의 모든 단어 벡터들
• 벨류(Value) :  입력 문장의 모든 단어 벡터들

키, 쿼리, 벨류가 모두 입력 시퀀스 벡터이다.

 
그렇다면 도대체 왜 자기 자신에게 어텐션 하는걸까?
 
위의 그림을 보자. 입력 데이터는 "The animal didn't cross the street because it was too tired." 이다. 해석해보자. "그 동물은 길을 건너지 않았다. 왜냐면 그것은 너무 피곤했기 때문이다." 
 
그것이 피곤했다.. 그것이 뭘까? 길일까 동물일까?  사실 인간에게는 너무나도 쉬운 문제이다. 길이 피곤할리가 없기 때문에, 자연스럽게 동물이 피곤했다고 이해할 것이다. 하지만 기계는 이것을 파악하는 것이 힘들다. (인간에게 쉬운 것이 기계에겐 어렵고 기계에게 쉬운 것은 인간에게 어렵다.. 모라벡의 역설이었나?)
 
본론으로 돌아와서 우리는 기계가 "그것"을 "동물"이라고 판단하길 원한다. 따라서, 기계가 문장 안에서 단어들의 연관성을 파악할 수 있도록 self-attention을 하는 것이라 생각하면 된다.
 
Self-attention은 계산 복잡도 측면에서도 다른 모델들에 비해 우수한 성능을 보였다.

 
위의 표를 보자.

• n : 시퀀스의 길이
• k : convolution의 커널 사이즈
• d : 차원
• r : restricted self attention에서의 neighborhood 사이즈

1행의 self-Attention을 보면, Complexity per Layer는 n^2*d의 시간복잡도를 가진다. (보통 n이 d의 값보다 작기 때문에 self-attention이 recurrent 모델보다 우수하다는 것을 알 수 있다.)
2열의 Sequential Operations는 multi-head를 통해 병렬화가 가능하므로 Sequence길이가 아무리 길더라도 동시에 연산을 수행할 수 있고, O(1)의 시간복잡도를 가진다.
3열의 Maximum Path Length는 Long-Term dependency와 관련이 있는데(학습이 잘되는가), 단어 사이의 거리가 멀더라도 Query와 Key를 설정하여 계산하므로 O(1)를 갖는다.(학습시키기 쉽다.)
 
 

2-3. Scaled Dot-product Attention

 
논문에서 저자는 어텐션 방식으로 "Scaled Dot-product Attetion"을 채택했다. 단순히 dot-product attention에서 scaler만 추가한 방식이다.

 
위의 수식을 잘보면 "scaled dot product" 어텐션 메커니즘이 기존과 다른점은 쿼리와 키의 내적값에 스칼라(키의 차원의 루트값)를 곱해준다는 것 뿐이라는 것을 알 수 있을 것이다.
 
논문에 따르면 d_k 값이 작으면 dot product 어텐션 방식과 additive 어텐션 방식이 비슷한 성능을 보이지만, d_k 값이 클 때 additive 어텐션 방식이 dot product 어텐션 방식보다 outperform 했다고 한다. 저자가 추측하기로는  큰 d_k 값에 대해 내적의 크기가 크게 증가하여 소프트맥스 함수를 기울기가 매우 작은 영역으로 밀어 넣었다고 생각했다. 이 효과를 상쇄하기 위해, 저자는 루트 d_k로 내적값을 나누었다.

 
 
2-4. Multi-Head Attention

 
저자는 어텐션 함수에 d_model 차원의 쿼리, 키, 벨류를 사용하는 것 대신에 h번의 서로 다른 학습된 linear projection으로 d_q, d_k, d_v 차원에 project 하는 것이 더 효과적이라는 것을 알아내었다. 이들은 병렬적으로 어텐션 함수를 거쳐 d_v 차원의 아웃풋 값을 출력할 수 있었다고 한다. 마지막으로 이들은 concatenated되어 다시 한번 project 된 다음 최종 결과 값을 만든다. 
 
사실 말이 어렵지 식으로 보면 이해하기 쉽다.

 
저자는 h를 8로 설정했다.(h가 head의 수를 나타낸다. 따라서 multi-head attention이라는 이름이 붙었다.) d_model = 512 이므로, 8개의 head에 대해 키와 벨류의 차원은 64가 된다.

 

 

2-5. Applications of Attention

• 인코더-디코더 어텐션 레이어에서, 쿼리는 이전 디코더 레이어의 값이고 키와 벨류는 인코더의 결과값이다. 이는 디코더의 쿼리가 인풋 문장의 모든 단어를 어텐션할 수 있도록 한다.
• 인코더는 self-attention 레이어를 포함한다. 이 때 쿼리, 키, 벨류는 모두 같은 값을 갖는다. 따라서 입력 문장에 대해 모든 단어를 스스로 어텐션 할 수 있다.
• 디코더의 self-attention 레이어는 해당 포지션까지의 모든 단어를 스스로 어텐션한다. masking 기법으로, 해당 포지션 이후 값들에 -(infinite) 값을 주어 치팅을 방지한다.

 

2-6. Position-wise Feed-Forward Networks
 

어텐션 서브 레이어 이후에, ReLU 활성화 함수를 포함한 두 개의 선형 변환이 포함된 Position-wise Feed-Forward Networks을 진행한다.(위 식 참조) 이는 모든 포지션에 따로따로, 동일하게 적용된다.
 
linear transformation은 다른 포지션에 대해 동일하게 적용되지만 레이어마다 parameter를 다르게 설정한다.
 
 

2-7. Embeddings and Softmax
 

다른 시퀀스 모델과 비슷하게, 학습된 워드 임베딩 모델을 이용한다. 인풋과 아웃풋 토큰의 차원은 d_model = 512가 된다. 또한, 다음 토큰을 예측하기 위해 softmax 함수를 사용하여 가장 그럴듯한 단어를 출력한다. 트랜스포머는 두 개의 임베딩 레이어와 pre-softmax 선형 변환 사이에 같은 가중치의 matrix를 공유한다. (임베딩 레이어의 가중치에는 루트(512)를 곱하여 사용한다.)
 
 

2-8. Positional Encoding

트랜스포머는 recurrene, convolution를 사용하지 않기 때문에, 시퀀스 데이터의 순서를 파악하기 어렵다. 게다가 앞서 말했듯이 한 문장안에서 각 단어들의 위치는 중요하다. 단어가 어느 위치에 들어가있냐에 따라 뜻이 달라질 수 있기 때문이다. 따라서 단어에 위치 정보를 포함하여 임베딩하는 것이 필수적이다.
 

 
하지만 이런 위치 정보를 담고 있는 벡터를 생성할 때, 두가지를 고려해야 한다.

1. 인풋 문장의 길이나 단어에 상관 없이 모든 시퀀스의 위치값은 동일해야한다. 즉, 시퀀스가 변경되더라도 위치 정보를 담는 벡터는 일정해야 한다.
2. 모든 위치값은 크면 안된다. 만약 특정 단어의 위치값이 너무 커져버리면 임베딩된 단어와 위치 정보가 더해졌을 때 다른 단어들에 있어서 상대적으로 다른 단어간의 상관관계 및 의미를 유추하기 어려워진다. (즉 어텐션 하기 어려워진다.)

고려사항 1

 

고려사항 2

 
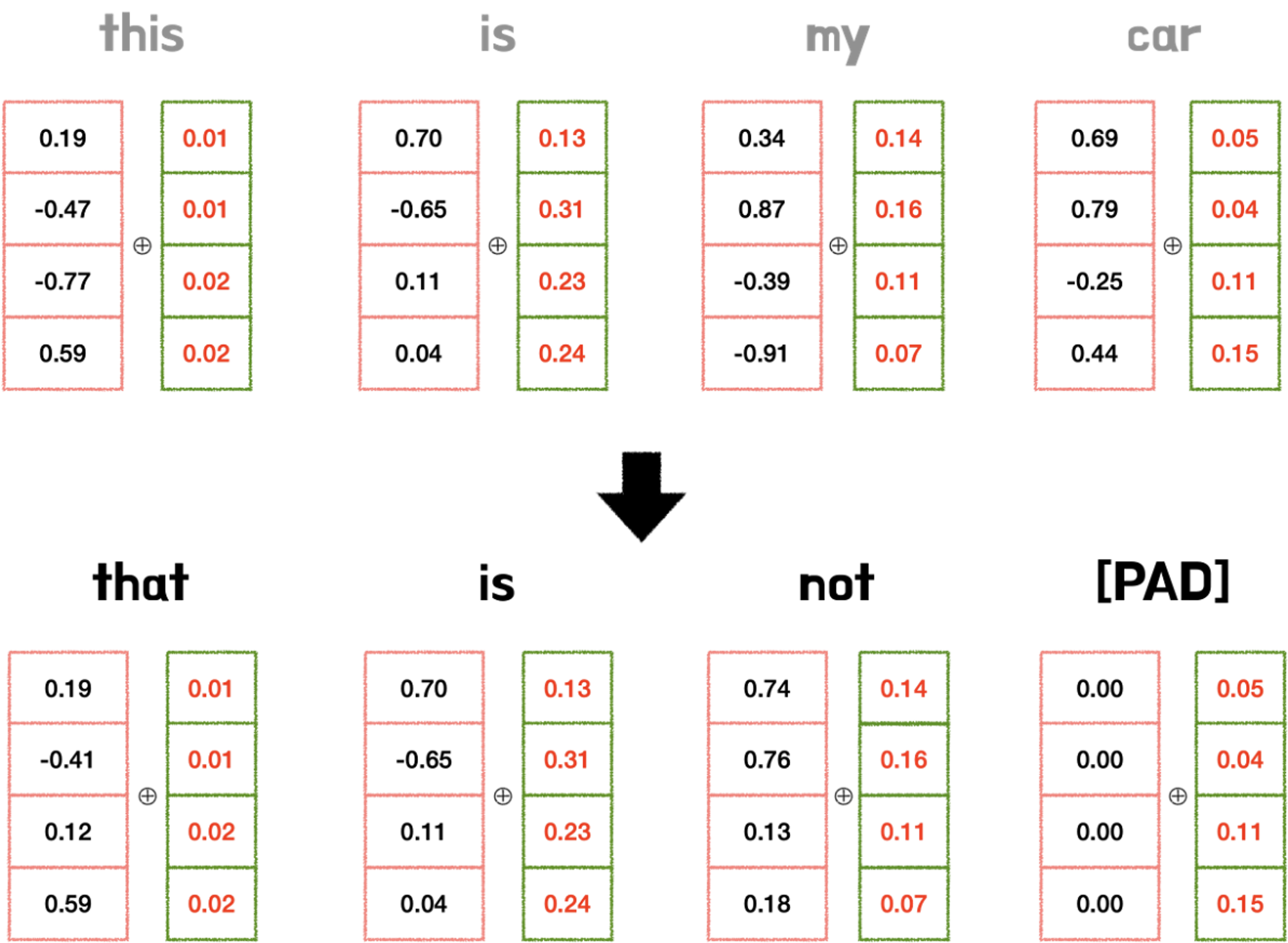
따라서 인코더와 디코더 스택 아래의 인풋 임베딩에 사인, 코사인 함수를 활용한 Positional Encoding을 적용하였다. 이러한 Positional Encoding은 인풋 임베딩처럼, 같은 차원 (d_model = 512)을 가져서, 둘을 더할 수 있게 하였다.
 

 
pos는 포지션이고, i는 차원을 의미한다. (아래 그림에서 각각 행과 열이라고 이해해도 된다.)

 
 
 
 
다음 포스팅에서는 트랜스포머를 이용한 간단한 코드 구현을 진행해보자.
 
끝!