Logical Scribbles
[딥러닝] Batch-Nomalization(배치 정규화)의 기초적 이해 본문
공부를 하며 Batch-Nomalization에 대한 정리를 해보았다.

다음과 같은 NN이 있다고 하자.
우리는 mini-batch를 이용하여 NN을 학습시킬 것이다.
하지만! 빨간 점(노드)에 들어오는 input의 distribution은 batch마다 변화할 수 있다. (직관적으로 내가 이해한 바로는 어떤 batch를 잡았을때 그 batch만의 특징이 있을 수 있으며 그 batch마다 고유의 distribution이 있을 것이다. 결론은 이게 NN의 학습에 안좋다고 한다.)
따라서 output의 distribution도 batch마다 변화할 수 있을 것이다.

가령 Update 마다 이러한 분포를 가진 input이 들어온다고 할 때, 이러한 batch의 고유한 distribution은 학습 과정에 방해가 되며 학습을 느리게 만든다.(작은 학습률을 사용해야하고, 신중한 가중치 초기화를 해야하는 등..)
이러한 현상을 "internal covariate shift" 라고 부르며, 입력의 분포를 nomalize함으로써 해결할 수 있다고 한다.
이렇게 nomalize된 입력들을 이용하여 NN을 학습시키게 되면, 상대적으로 높은 학습률과 가중치 초기화에 신경을 덜 써도 된다고 한다.

그러면 어떻게 batch의 데이터들을 nomalize할 수 있을까?
예를들어 mini-batch의 size를 4라고 해보자. 즉, 1개의 batch당 4개의 data들이 묶여서 들어온다는 것이다.
이 4개의 데이터들에 대해서 평균과 분산을 구해준다. (중학교 수학이다.)
그 후, 각각의 데이터들을 Nomalization 해준다. (고등학교 수학이다.)

이 부분에서 약간의 문제가 발생한다. 분자의 (net - 평균) 부분을 잘 생각해보자.
원래의 (nomalized 안된) data들의 net을 계산할 때, 우리는 WX+b 라는 식을 이용한다. (X는 input)
그리고, 고등학교 확률과 통계 과목을 잠깐 remind해보면, E(net)은 E(WX)+b와 동일하다는 것을 알 수 있다.
따라서 분자 (net-평균)을 계산할 때, (WX+b) - (E(WX)+b) 라는 과정을 거치게 된다.
위 식을 정리해보면, WX-E(WX)가 나온다. (이 곳에서 이상함을 느껴야하나보다. NN에서는 Bias가 매우 중요하다고 하는데, 아직 왜 그것이 중요하고 어떻게 활용되는지는 자세히 모르겠고 더 공부하여 업데이트 하도록 하겠다.)
따라서
batch를 nomalization 한 뒤 NN을 학습시킬 때 nomalization 된 data들이 한 번더 특수한 계산(?)을 당하고, Activation Function에 통과된다.

즉, 정규화된 데이터에 감마를 scaler로, 베타를 shifter 계수로 사용하여 한번더 데이터 처리를 해주는 것이다.
내가 이해한 바로는, 데이터들이 정규화 되면 Sigmoid (Activation Function) 상에서 원점 주변에 흩뿌려지게 되는데, Sigmoid 함수에서 원점 주변의 그래프 모양을 기억해보면 Linear한 느낌(?)을 갖음을 알 수 있다.
따라서 감마와 베타를 이용하는 것은, 원점 주변으로 뿌려진 데이터들을, linearity를 없애기 위해 다시 손으로 고르게 뿌려주는 행위라고 이해했다.
감마와 베타는 HyperParameter가 아니다. 즉 학습률처럼 우리가 manually 설정해야할 대상이 아니다. 쉽게 말하면 얘네들도 학습대상이고, Batch Nomalization 학습에서 학습대상은 가중치,감마,베타이다.
지금까지 Training 과정을 살펴보았고, 이제부터는 Testing 과정에서 이렇게 학습시킨 NN을 어떻게 평가할 것인지 살펴보자.
Testing 과정에서는 어떤 데이터들의 평균과 분산이 사용되어야 할까? (즉, 어떠한 평균과 분산을 이용하여 정규화 해야할까?)
답은 Training 할 때 계산해 두었던 Batch들의 평균들과 분산들을 고대로 이용하는 것이다. (약간의 계산을 하긴한다.)
평균은 Batch들의 평균을 다시 한번 평균내어 사용하고, 분산은 각 배치의 데이터 수 m을 이용하여 각 batch의 분산에 m/(m-1)을 곱해준 뒤 그들을 평균낸다.
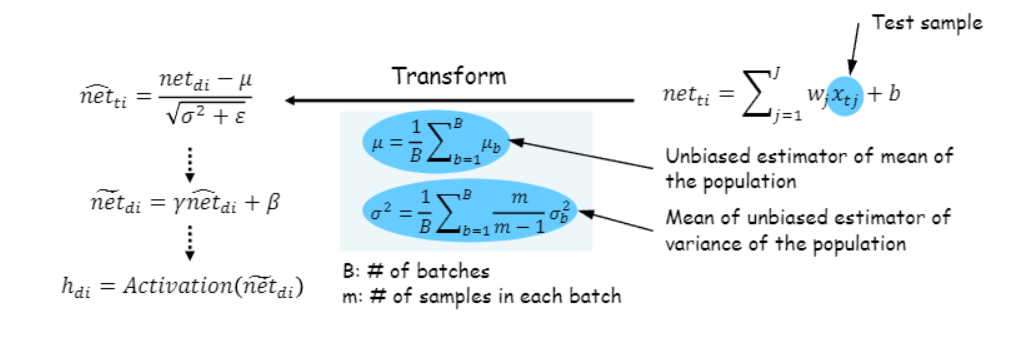
다시 과정을 설명해보면, 어떠한 test sample이 주어졌을 때, 원래 하던대로 net을 계산한다.
그 뒤, 새롭게 구한 평균과 분산을 이용해서 net을 정규화를 해준다!
이를 학습된 감마와 베타를 이용하여 net을 한번 더 계산해주고, Activation Function에 집어넣는다.
이러한 Batch-Nomalization의 장점으로는, 앞서 언급했던 internal covariant shift를 해결하는 효과가 있다. 또한 모델을 regularization 하는 효과가 있어 overfitting을 방지하며, 훨씬 큰 학습률을 사용할 수 있어 학습 속도를 개선시킬 수 있다. 또 가중치 초기화에 훨씬 덜 민감하다고 한다.
'딥러닝 > 딥러닝 이론' 카테고리의 다른 글
| [최적화] 서포트 벡터 머신(SVM)은 Convex 문제? (0) | 2023.11.18 |
|---|---|
| [객체 탐지] 2-Stage Dectector 와 1-Stage Detector (0) | 2023.11.18 |
| [최적화] Basic Inequality의 증명 (0) | 2023.11.15 |
| [객체 탐지] HOG(Histogram of Oriented Gradient for human detecting)에 대하여 (1) | 2023.11.14 |
| [객체 탐지] IoU(Intersection over Union), mAP(Mean Average Precision)이란? (0) | 2023.11.13 |




