Logical Scribbles
[객체 탐지] IoU(Intersection over Union), mAP(Mean Average Precision)이란? 본문
[객체 탐지] IoU(Intersection over Union), mAP(Mean Average Precision)이란?
KimJake 2023. 11. 13. 23:26
Object Detection 관련 논문을 읽으면 거의 무조건 나오는 IoU와 mAP에 대해 알아보도록 하자.
물론 나도 mAP에 대한 개념이 정확하지 않아서 공부하는겸 작성하는 글이므로, 오류가 있으면 지적 바란다.

1. IoU
머신러닝을 공부해 본적 있다면 IoU는 한번쯤 들어보았을 것이다.
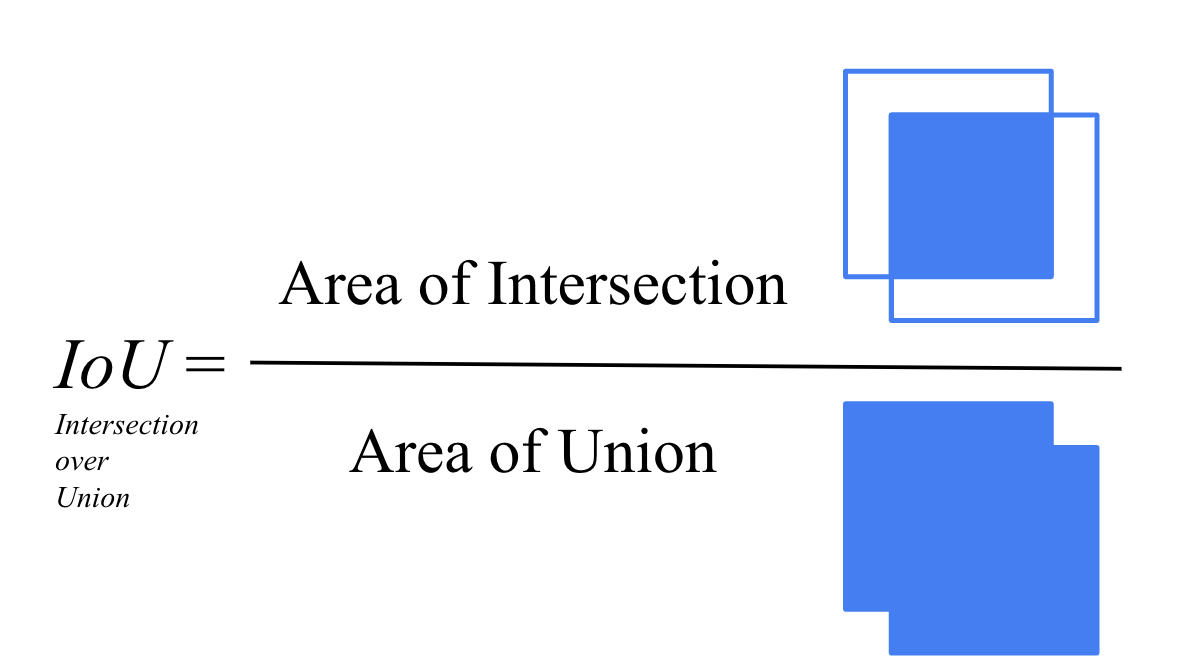
간단히 말해서 IoU란, 정답 영역과 예측 영역이 얼만큼 겹쳐져 있는지를 평가하는 지표이다.
당연히 IoU가 크면 모델이 object detection을 잘한다는 해석을 할 수 있을 것이다. 수식으로 표현하면 다음과 같다.

분모는 각 영역의 넓이를 더한 후 겹치는 영역의 넓이를 1번 빼준 것이고 (왜냐하면 두 영역의 넓이를 더하면 겹치는 영역이 2번 더해지는 꼴이기 때문), 분자는 겹치는 영역의 넓이이다.
2. mAP
mAP의 이해를 위해선 2가지의 사전 지식이 필요하다. 각각 알아보자.
- Precision Recall 곡선
- Average Precision
2-1.Precision Recall 곡선
precision과 recall을 알기 위해선 TP, FN, FP, TN에 대해 알아야한다. 옛날 수능 국어 지문에서 위양성, 위음성 같은 개념이 나왔던 것 같은 기억이 있는데, 그 개념이다.

여기서 Precision이란, 예측 결과가 얼마나 정확한지를 나타내는 지표이다. 유명한 예시를 들자면, 의사가 환자를 코로나라고 진단 내렸을 때 정말 그 사람이 코로나 환자인 비율이다.
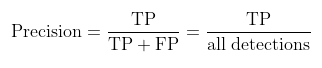
또한 Recall이란, Ground Truuth 중에서 얼마나 정답을 맞추었는지를 나타내는 지표이다. 즉 모든 코로나 환자 중에서 코로나 환자임에도 불구하고 코로나에 걸리지 않았다고(음성) 진단 받은 환자가 있을 때, 전체 코로나 환자 중 의사가 코로나 환자라고 진단한 사람의 비율을 나타낸다.

Precision과 Recall은 반비례 관계를 갖는다.
이를 바탕으로 기계에게 15개의 물체에 대한 Precision과 Recall을 계산하라고 하면,

confidence 값에 따라 이러한 결과를 도출해낸다. 이에 따라 출력 되는 아웃풋 수를 조절할 수 있는데, 위의 그림에서는 confidence를 10%정도로 설정한 듯 하다. 이렇게 confidence가 10%일 때, Precision과 Recall의 비율은 각각 0.7과 0.47이라고 한다. 만약 confidence를 70%로 설정하면 I,E,D,J,B에 대한 Precision과 Recall만이 출력될 것이다.
이제 달라지는 confidence 값에 대한 Precision Recall 그래프를 그리자!

이것이 바로 Precision Recall 곡선이다.
2-2. Average Precision
심플하게 말하면 PR curve에서 계단 형식(단조 감소 함수)으로 다시 그린 그래프의 밑넓이를 Average Precision 이라고 한다.
이 때, 11점 보간법이 사용된다.

2-3. mAP
Object Detection task에는 class가 여러개 있을 것이다. 각 클래스마다 AP를 구하고, 모든 클래스에 대해 더한 뒤 클래스의 개수로 나눠주면, 그것이 mAP이다! (즉 클래스들의 AP의 평균)
끝!
'딥러닝 > 딥러닝 이론' 카테고리의 다른 글
| [최적화] 서포트 벡터 머신(SVM)은 Convex 문제? (0) | 2023.11.18 |
|---|---|
| [객체 탐지] 2-Stage Dectector 와 1-Stage Detector (0) | 2023.11.18 |
| [최적화] Basic Inequality의 증명 (0) | 2023.11.15 |
| [객체 탐지] HOG(Histogram of Oriented Gradient for human detecting)에 대하여 (1) | 2023.11.14 |
| [딥러닝] Batch-Nomalization(배치 정규화)의 기초적 이해 (0) | 2023.10.29 |




