Logical Scribbles
[선형대수학] 역행렬의 의미 (Feat. 행렬식) 본문
지난 포스팅에서는 행렬식의 기하학적 의미에 대해 살펴보았다.
[선형대수학] 행렬식의 기하학적 의미
이번 포스팅에서는 선형대수학에서의 행렬식에 대해 알아보도록 하자.행렬식 (Determinant) Determinant 라고도 불리는 행렬식의 notation은 다음과 같다.이제부터 우리는 '정방행렬'에 주목할 것이다.
stydy-sturdy.tistory.com
이번에는 이 행렬식의 기하학적 의미의 연장선상에서 역행렬을 바라보려고 한다.
간단하게 역행렬이란 정방행렬의 역원이다. 수학적으로 'X의 역원'이란 X와의 정의된 연산을 통해 결과값이 항등원이 되는 것을 말한다. 실수 관점에서 3의 덧셈 역원은 3과 덧셈 연산이 이루어져 덧셈 항등원 0이 나오는 수, 즉 -3이고 3의 곱셈 역원은 3과 곱셈 연산이 이루어져 곱셈 항등원 1이 나오는 수라고 생각할 수 있겠다.
이 역원에 대한 개념을 행렬 관점으로 보면 , 행렬 A의 역원이란 행렬 A와의 연산을 통한 결과값이 항등행렬이 되는 행렬을 말한다고 생각할 수 있겠다. 우리는 그러한 행렬을 역행렬이라고 부르기로 약속한 것이다.
만약 행렬을 선형변환으로 본다면 특정한 선형변환 A와의 연산을 통해 결과값이 항등원이 되는 선형변환이 A의 역행렬이라고 생각할 수 있다.
이번에도 정방행렬을 메인으로 다룰 것이다. 행렬식부터 시작해서 이번 역행렬까지 정방행렬에 대해 다루고 있는 이유는 행렬식과 역행렬이 정방행렬에서만 정의가 되기 때문이다. (기회가 되면 정방행렬이 아닐 때의 유사역행렬에 대해 다루기로 하겠다.)
먼저 2X2 정방행렬에서의 역행렬 공식을 살펴보자.

이렇다고 한다. A의 역행렬 공식을 보고 뭔가 익숙한 것이 보였다면 이전 포스팅 행렬식을 잘 따라온 것이다.
지난 포스팅에서 행렬식은 선형변환 된 후 새로운 기저가 이루는 면적의 변화를 나타내는 스칼라 값이라고 했다. 그리고 2X2 정방행렬의 행렬식 값은 다음과 같은 공식으로 구할 수 있었다.

이제 위의 식과 역행렬의 공식을 비교해보자. 역행렬 공식에 존재하는 행렬의 계수가 바로 행렬식의 역수인 것을 발견할 수 있을 것이다. 이것이 우연일까?
어찌됐든 A의 역행렬도 행렬이다. 다시 말하면, A의 역행렬도 결국 선형변환이라는 것이다!
A는 선형변환이고, A의 역행렬도 선형변환이다. 즉 A는 기저를 새로운 기저로 바꾸는 변환이고, A의 역행렬도 어떠한 기저를 새로운 어떠한 기저로 바꾸는 선형변환일 것이다. 그리고 직관적으로 A의 역행렬은 뭔가 A와 관련이 있는 선형변환일 것임을 느낄 수 있다.
그렇다면 A의 역행렬이 의미하는 것은 무엇인가? 결국 A의 역행렬은 A에 의한 선형변환의 역-선형변환 과정이다. 지난 포스팅에서 보았던 GIF를 다시 봐보자.

행렬에 의해 어떠한 기저가 새로운 변화로 변하는데, 이를 뒤로감기 한다고 상상 해보면, 어떤 변형된 기저를 다시 원래의 기저로 변하게 하는 선형변환이 바로 A의 역행렬이라는 것이다.

x벡터가 선형변환 A에 의해 v벡터가 되었다고 생각해보자. x벡터를 다시 구하고 싶다면 어떻게 해야 할까? 직관적으로 선형변환의 역과정을 벡터v에 취해주면 될 것임을 알 수 있을 것이다. 이를 수식으로 표현하면 다음과 같다.

이처럼 역행렬은 기존의 선형변환의 역과정이라고 생각하면 된다. 예를들어 기저를 왼쪽으로 90도 회전시키는 행렬이 존재한다고 했을 때, 이의 역행렬은 기저를 다시 오른쪽으로 90도 회전시키는 선형변환일 것이다.
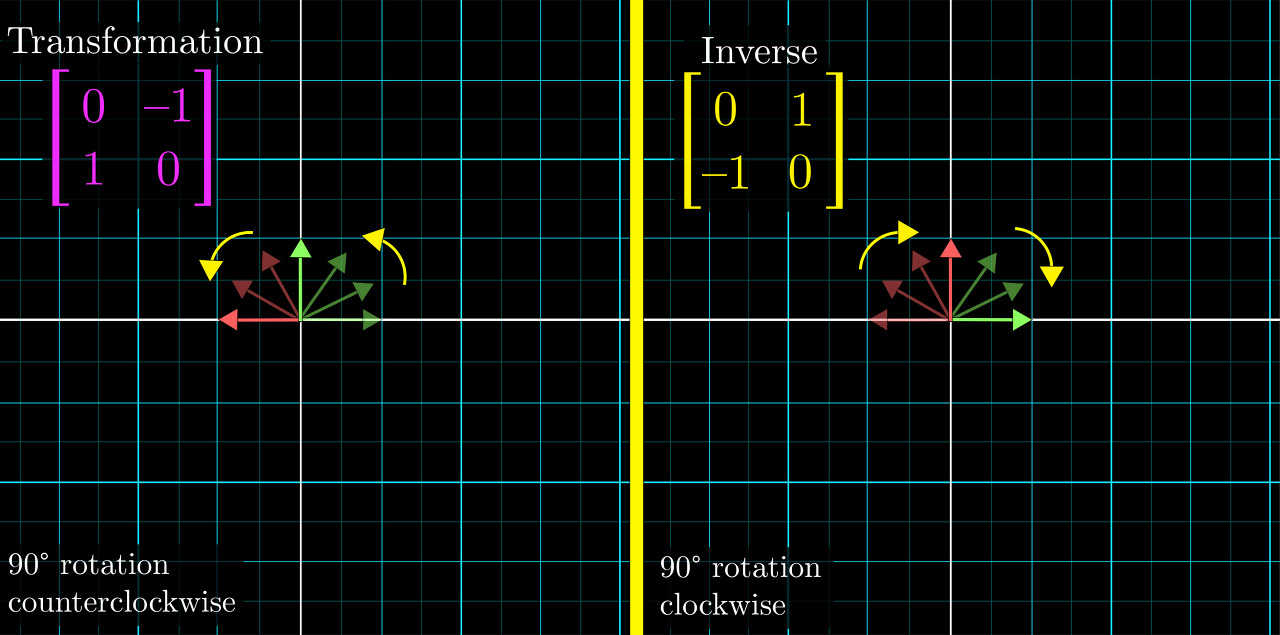
행렬식은 기존의 기저가 변화했을 때의 단위 넓이 변화이다. 만약 선형변환에 의한 변화(기저, 기저가 이루는 면적 등등)를 원상태로 되돌리고 싶을 때, 넓이 변화도 원상복구 해주어야 할 것이다. (혹은 처음의 넓이로 다시 변환해야 할 것이다.) 그러면 확대되거나 축소된 넓이를 다시 기존값으로 만들어야하는데, 간단하게 여기서 행렬식의 역수 값이 사용되는 것이다.
따라서 2X2 정방행렬의 역행렬 공식에 기존 행렬의 행렬식의 역수값이 곱해져 있는 것이다!
또 한가지 중요한 이야기를 더 해보자.
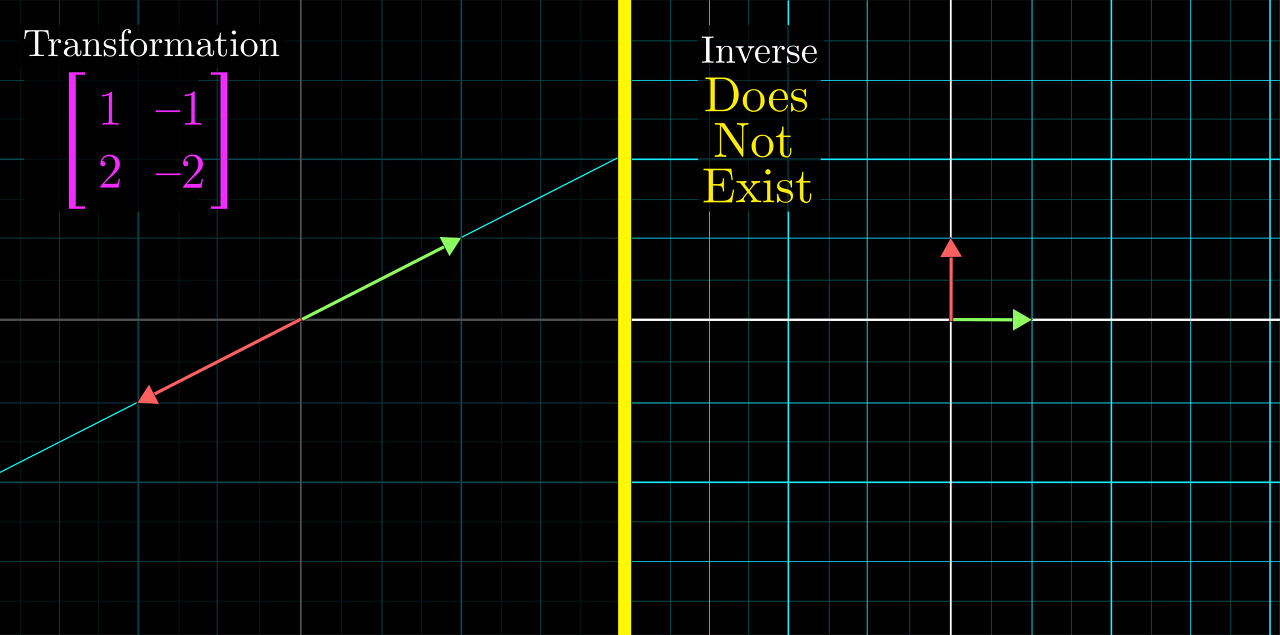
행렬식이 0이면 기저가 표현하는 모든 공간이 더 낮은 차원으로 쪼그라드는 것이고, 그러면 넓이 변화를 되돌려 줄 때 넓이 변화 행렬식의 역수 분모에 0이 쓰여야하는 것이다. 하지만 분모가 0일 수는 없다.
따라서 매우 중요한 결론을 얻을 수 있다.
행렬식이 0이면 역행렬은 존재하지 않는다. 즉, 어떤 선형변환이 벡터들을 낮은 차원으로 쪼그라들게 할 때, 그 과정을 다시 되돌려놓는 선형변환은 존재하지 않는다는 것이다.
마지막으로 이러한 역행렬의 의미를 한번에 보여주는 GIF를 첨부하며 마무리한다.
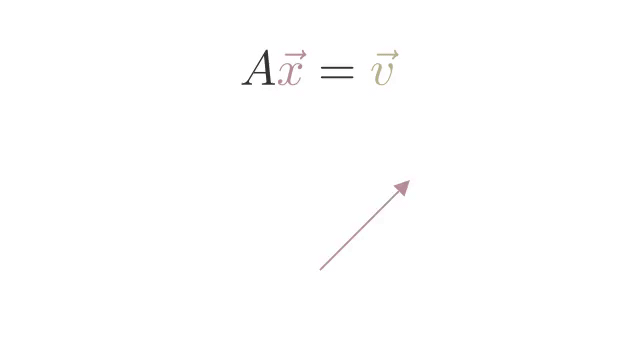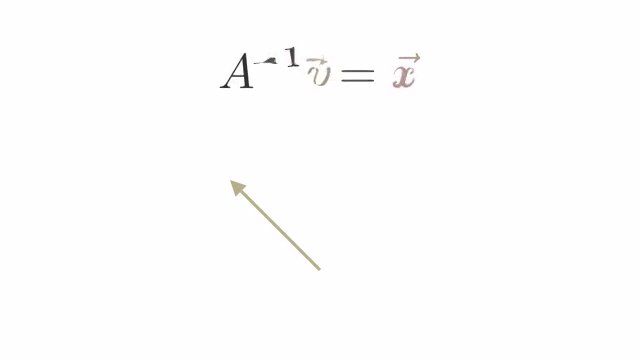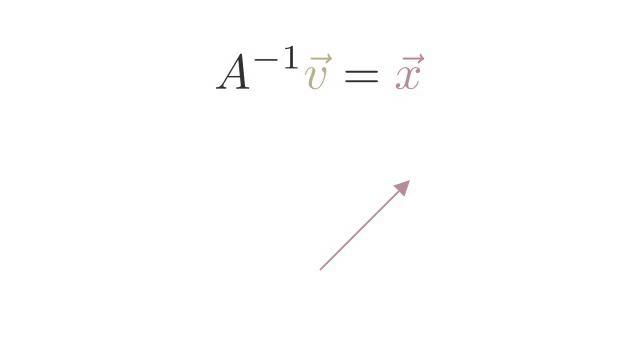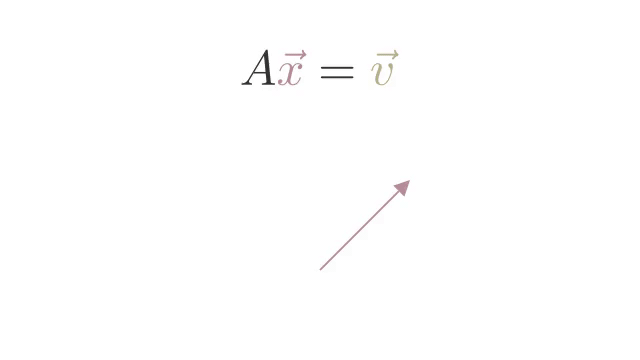
끝!
'기초 수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 고유값 분해 (0) | 2023.11.19 |
|---|---|
| [선형대수학] 고유값(Eigenvalue)과 고유벡터(Eigenvector) (0) | 2023.11.18 |
| [선형대수학] 행렬식의 기하학적 의미 (0) | 2023.11.17 |
| [선형대수학] 행렬 곱의 여러가지 해석 (0) | 2023.11.17 |
| [선형대수학] 선형변환과 행렬 (0) | 2023.11.17 |




