Logical Scribbles
[선형대수학] 행렬 곱의 여러가지 해석 본문
수학적으로 행렬의 곱을 어떻게 계산하는지는 다들 알고 있을 것이라 생각한다.

나는 고등학교 '고급수학' 과목에서 처음으로 행렬 곱을 배웠었는데, 그 때 선생님께서 행렬 곱은 '드르륵, 드르륵' 이라고 설명해주신 것이 기억에 남고, 단순하게 행렬 곱을 구해야 할 때는 아직도 그런 방식이 가장 편하다.
이번 포스팅에서는 이 행렬 곱의 일반적인 방법에 대해 살펴보고, 행렬 곱을 '열벡터의 선형결합' 이라는 관점으로 이해하는 법 그리고 행렬 곱의 기하학적 의미에 대해 알아보자.
1. 일반적인 행렬의 곱셈

행렬 곱에 대한 정의이다. 위의 식을 살펴보면 A와 B행렬을 곱해서 나온 C행렬의 i번째 행, j번째 열은 (A의 i행 1열의 원소) * (B의 1행 j열의 원소) + (A의 i행 2열의 원소) * (B의 2행 j열의 원소) + ... 의 계산을 통해서 나온다는 것이다.
사실 이해가 잘 되지 않는다. 더 친절하게 설명을 해보면, 행렬 A와 B를 곱한 행렬 C의 i행 j열의 값은, A의 i번째 행의 원소들과 B행의 j번째 열의 원소들을 하나하나씩 곱해서 더해서 구하자는거다. 이를 그림으로 표현하면 다음과 같다.

이를 잘 생각하고 이해해보면 행렬의 각 원소값은 벡터의 내적을 표현한 것임을 알 수 있다. 이 관점이 왜 중요한지에 대해서 나중에 설명할 기회가 있다면 글을 작성해보도록 하겠다.
2. 행렬 곱 = 열 벡터의 선형 결합
행렬 곱 하나를 계산해보며 시작하자.

위의 행렬 곱 문제를 어떻게 풀 것인가? 위에서 설명한 방법으로 계산을 진행하면 곧 다음과 같은 결과를 얻을 수 있다.

위의 행렬 곱을 다음과 같이 바라보자.

이는 행렬 곱을 앞의 행렬의 열벡터들의 선형결합으로 이해한 것이다. 벡터의 선형결합이 의미하는 것은 벡터공간의 생성이다. 즉, 위의 식이 의미하는 것은 "두 벡터를 어떻게 적절히 선형결합해야 [11,12]^T라는 벡터가 되는 것인가?" 이다. 그리고 그 '적절한' 선형결합에 필요한 계수가 3과 5인 것이다.
이제 아래의 수식을 이 관점에서 생각해보자.

이 식이 의미하는 것은, A의 열벡터가 생성하는 벡터공간에 b라는 벡터가 존재 하는가? (물론 그 벡터공간에 b가 존재하지 않을 수 있다.) 그리고 존재 한다면 어떻게 적절히 열벡터의 선형결합을 진행해야 하는가? 이다. 이때, '적절한' 선형결합의 계수가 x벡터의 원소가 될 것이다.
이제 아래 그림을 보자.
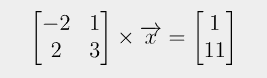
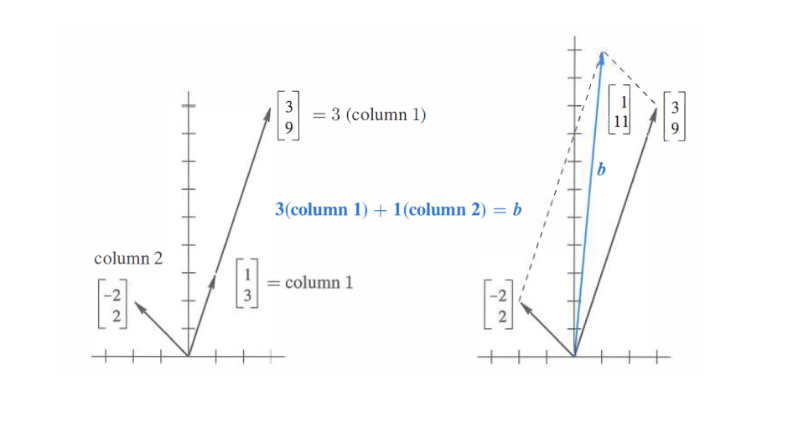
위 그림을 직관적으로 설명하면 '왼쪽 행렬에 어떤 벡터를 곱해야 오른쪽 벡터가 나오는가?' 이다.
이를 방금 설명한 방식으로 이해하면, '어떤 계수를 선택하여 [-2,2]^T와 [1,3]^T를 선형결합해야 [1,11]^T 벡터가 나오는가?' 이고, 그 계수는 각각 3,1이 되어 [3,1]^T가 x가 된다.
3. 행렬 곱의 기하학적 의미
https://stydy-sturdy.tistory.com/17
[선형대수학] 선형변환과 행렬
이번 포스팅에서는 선형변환에 대해 알아보자. 본격적으로 선형변환에 대해 알아보기 전, 행렬(Metrix)이 무엇인지부터 알아보도록 하자. 결론부터 말하면, 행렬은 선형변환이다. 선형변환이란
stydy-sturdy.tistory.com
이 글을 읽으면 더 이해가 잘 될 것이다. 저 글을 요약하면, 행렬은 곧 선형변환이고 행렬은 결국 기저를 새로운 기저로 변화시킨다는 것이다.
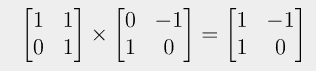
이제 이 행렬 곱을 살펴보자. 좌변의 첫번째 행렬과 두번째 행렬은 선형변환이다.
이제 두 변환을 함수로 생각하고, 곱셈은 합성이라고 생각해보자. 그러면 두 행렬의 곱은 합성함수가 되고, 좌변의 두번째 함수의 아웃풋이 좌변의 첫번째 함수에 들어갈 것이다.
이를 다시 '행렬은 선형변환이다'라는 관점으로 생각해보면, 먼저 좌변의 두번째 행렬을 통해 원래 기저의 선형변환이 이루어지고, 이 결과가 첫번째 행렬에 의해 한번 더 선형변환 됨을 알 수 있다. 그리고 신기하게도 그 결과가 우변의 한개의 선형변환과 같다는 것이다.
결국 두개의 순차적인 선형변환이 한개의 선형변환으로 퉁쳐질 수 있다는 것이다. 아래 GIF를 보자.
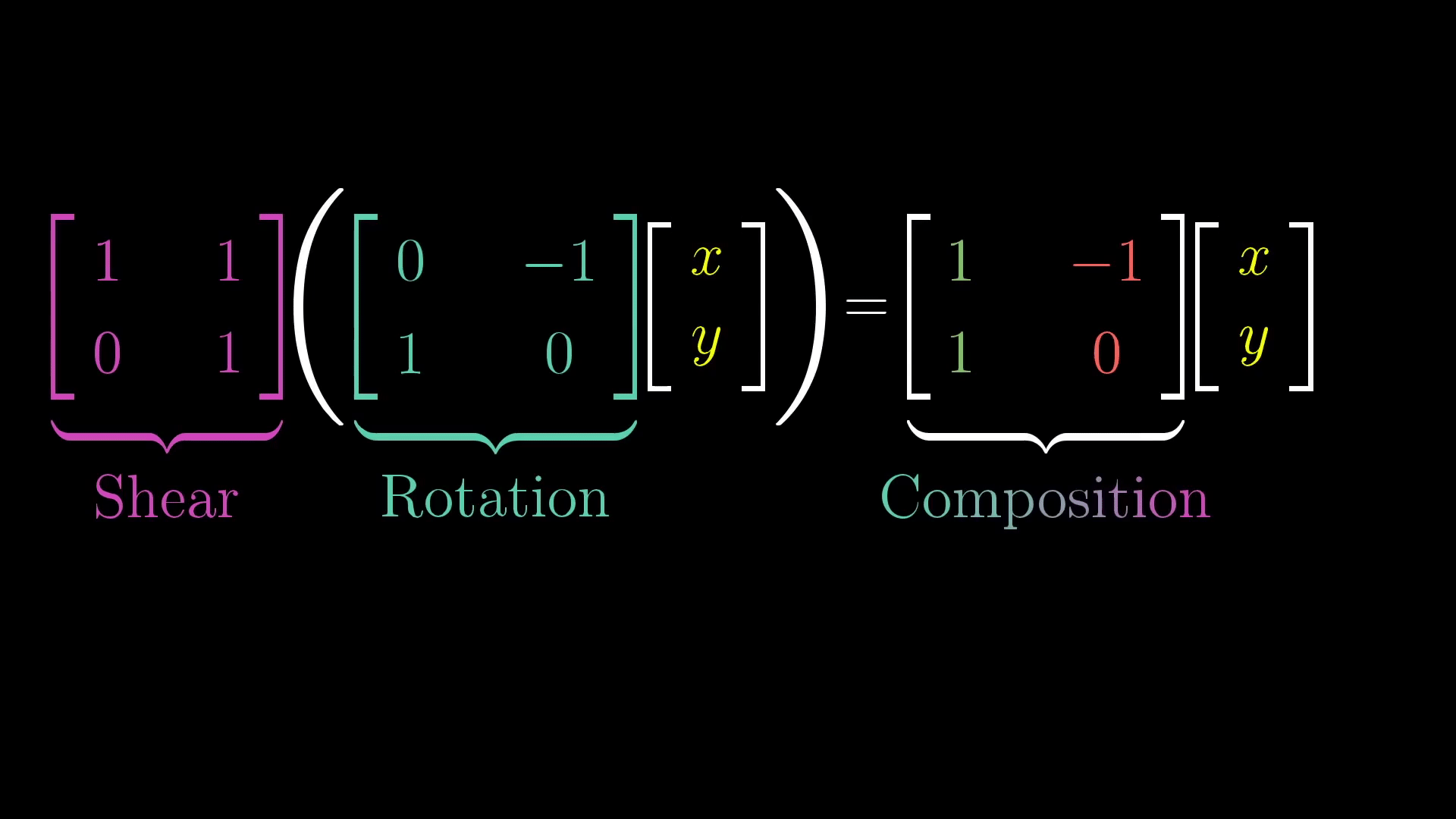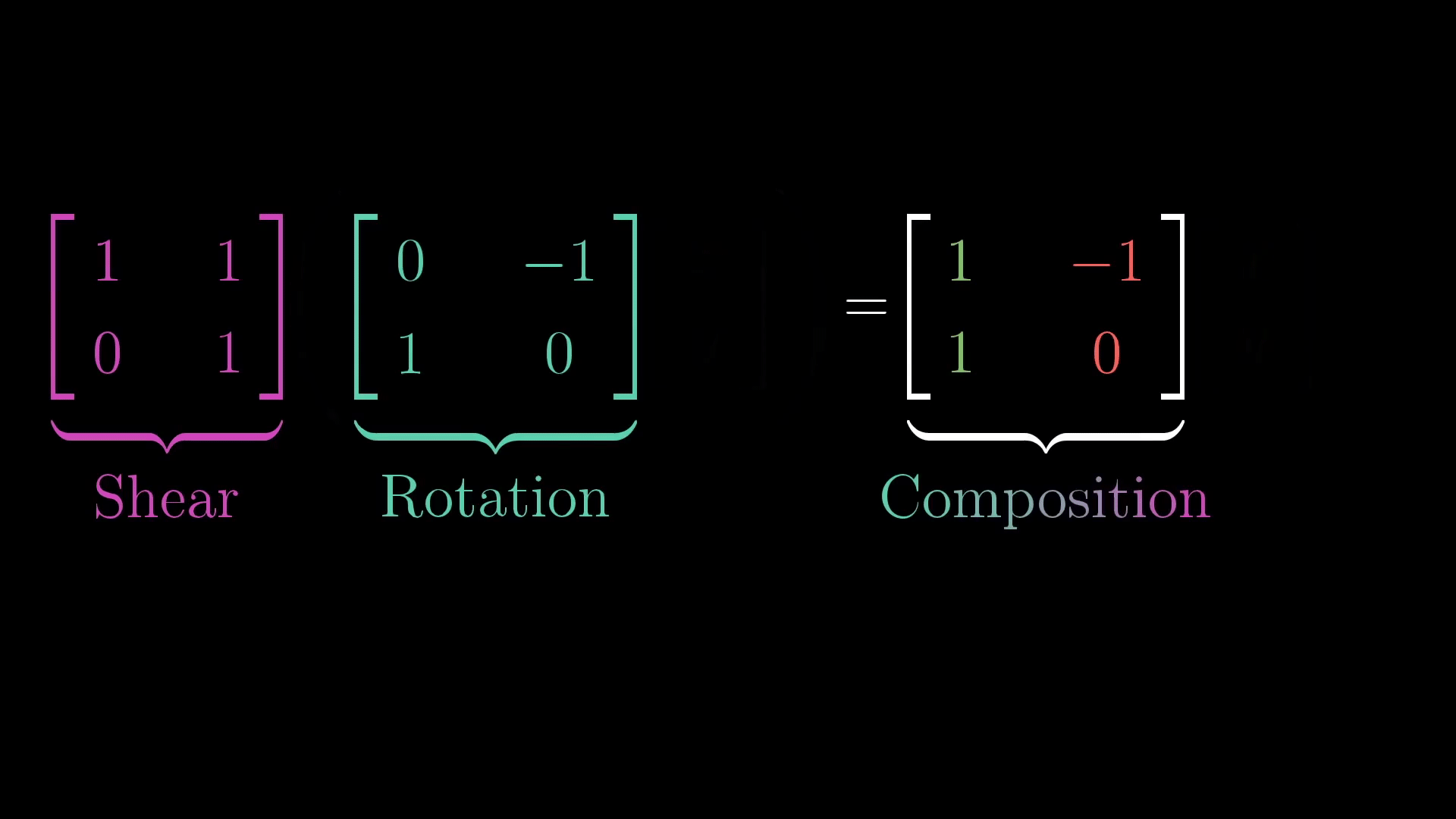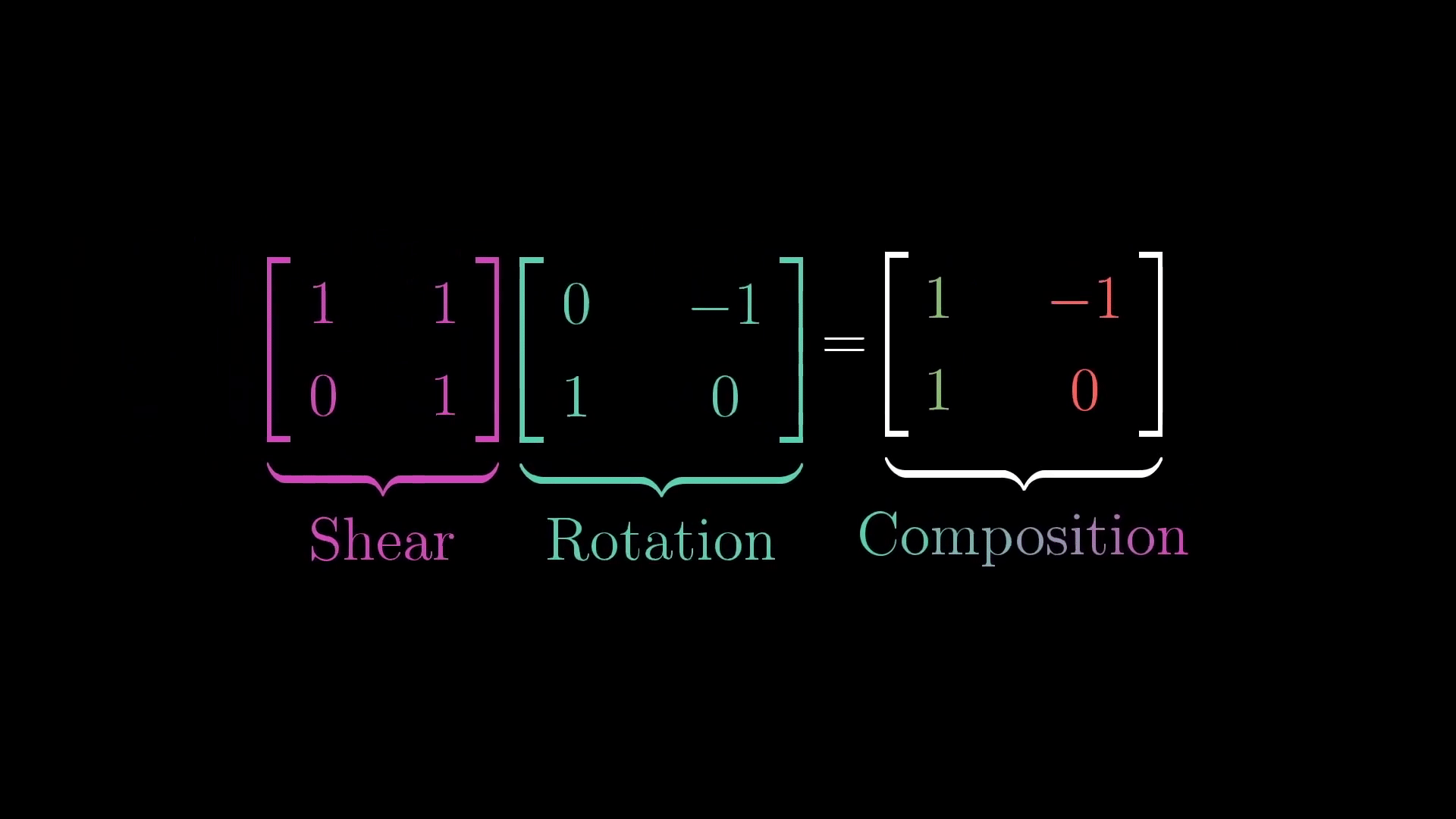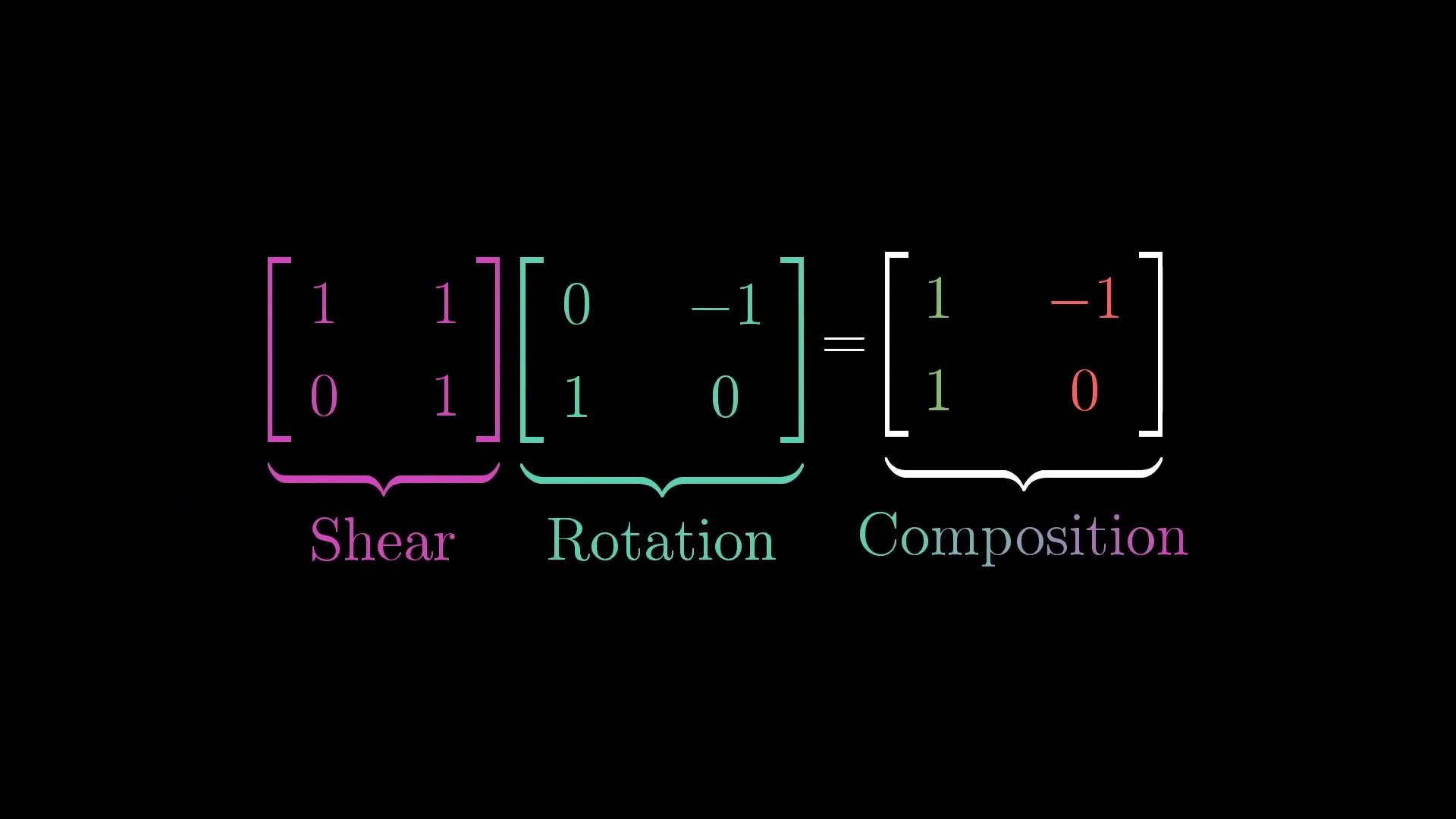
사실 앞서 소개한 좌변의 첫번째 행렬은 기저를 늘리는 선형변환이고, 좌변의 두번째 행렬은 기저를 회전시키는 선형변환이었다. 그리고 이게 합성되어, 우변의 선형변환이 되는 것이다. 이를 더 직관적으로 말하면 우변의 선형변환은 결국 '돌리고 늘리는 선형변환'이 되는 것이다!

이번 포스팅에서 소개한 아이디어들은 이후 선형연립방정식 풀이, 선형 회귀, SVD, PCA 등에 활용되므로 매우 중요하다.
끝!
'기초 수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 고유값 분해 (0) | 2023.11.19 |
|---|---|
| [선형대수학] 고유값(Eigenvalue)과 고유벡터(Eigenvector) (0) | 2023.11.18 |
| [선형대수학] 역행렬의 의미 (Feat. 행렬식) (1) | 2023.11.18 |
| [선형대수학] 행렬식의 기하학적 의미 (0) | 2023.11.17 |
| [선형대수학] 선형변환과 행렬 (0) | 2023.11.17 |




