Logical Scribbles
[선형대수학] 선형변환과 행렬 본문
이번 포스팅에서는 선형변환에 대해 알아보자. 본격적으로 선형변환에 대해 알아보기 전, 행렬(Matrix)이 무엇인지부터 알아보도록 하자.
결론부터 말하면, 행렬은 선형변환이다. 선형변환이란 다음 두가지를 만족시키는 변환 T이다.

따라서 어떤 특정한 벡터 (x,y)^T가 있을 때, 그 벡터에 대한 선형변환은 다음을 만족시킨다.

위 식에서 재미있는 점은 벡터 (1,0)^T 와 벡터 (0,1)^T는 R^2의 기저라는 것이다. 그러므로 위의 3번째 식을 'R^2의 기저를 선형변환 한 후, 각각 x배, y배 해서 더한 꼴' 이라고 받아들일 수 있을 것이다.
여기서 'R^2의 기저를 선형변환' 한 결과를 새로운 기저라고 생각해보자. 그러면 어떠한 벡터가 선형변환 되면 그 결과는 새로운 기저의 x배, y배의 합이 된다는 결론을 얻을 수 있다.
이제 밑의 GIF를 보자.
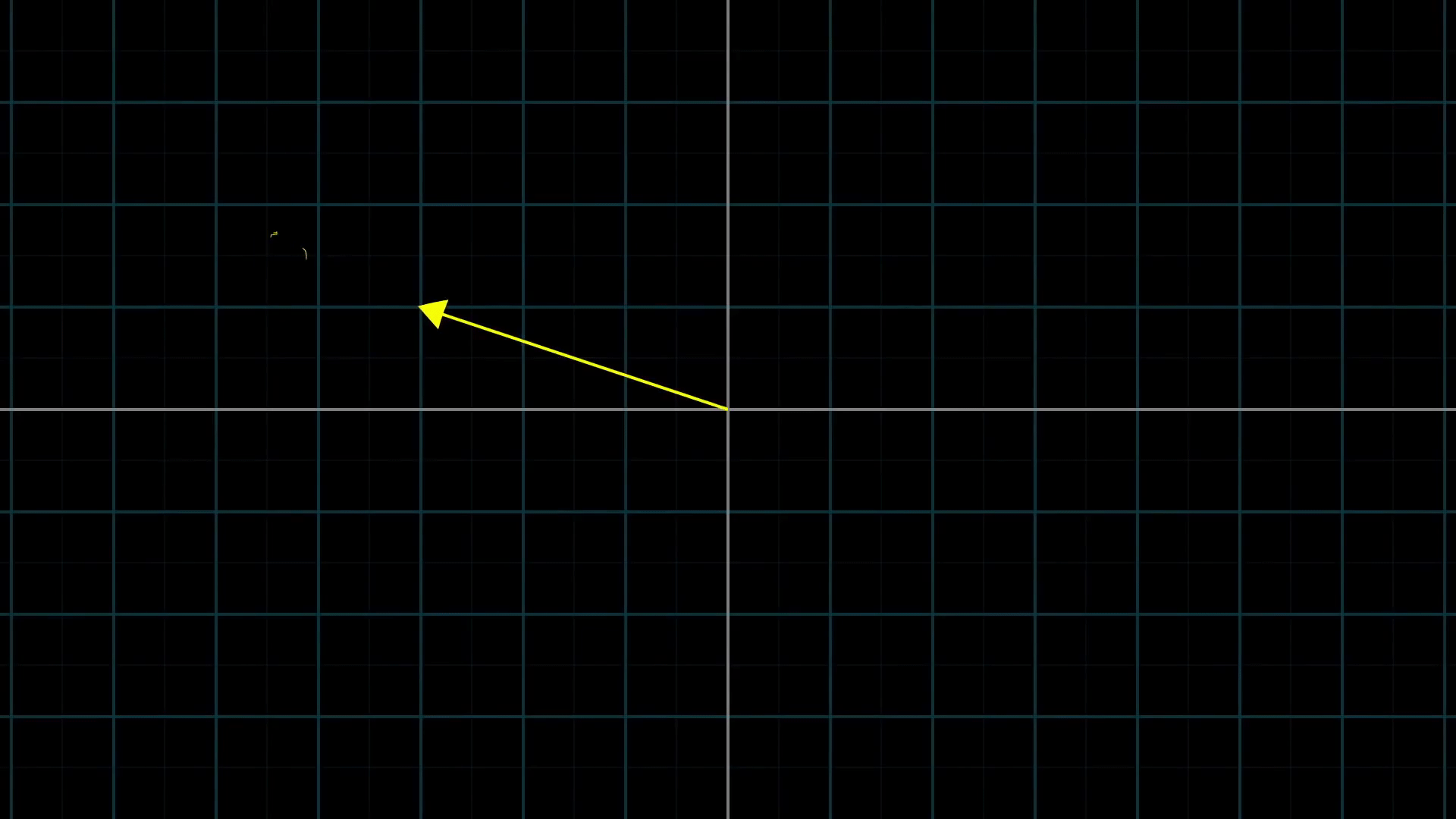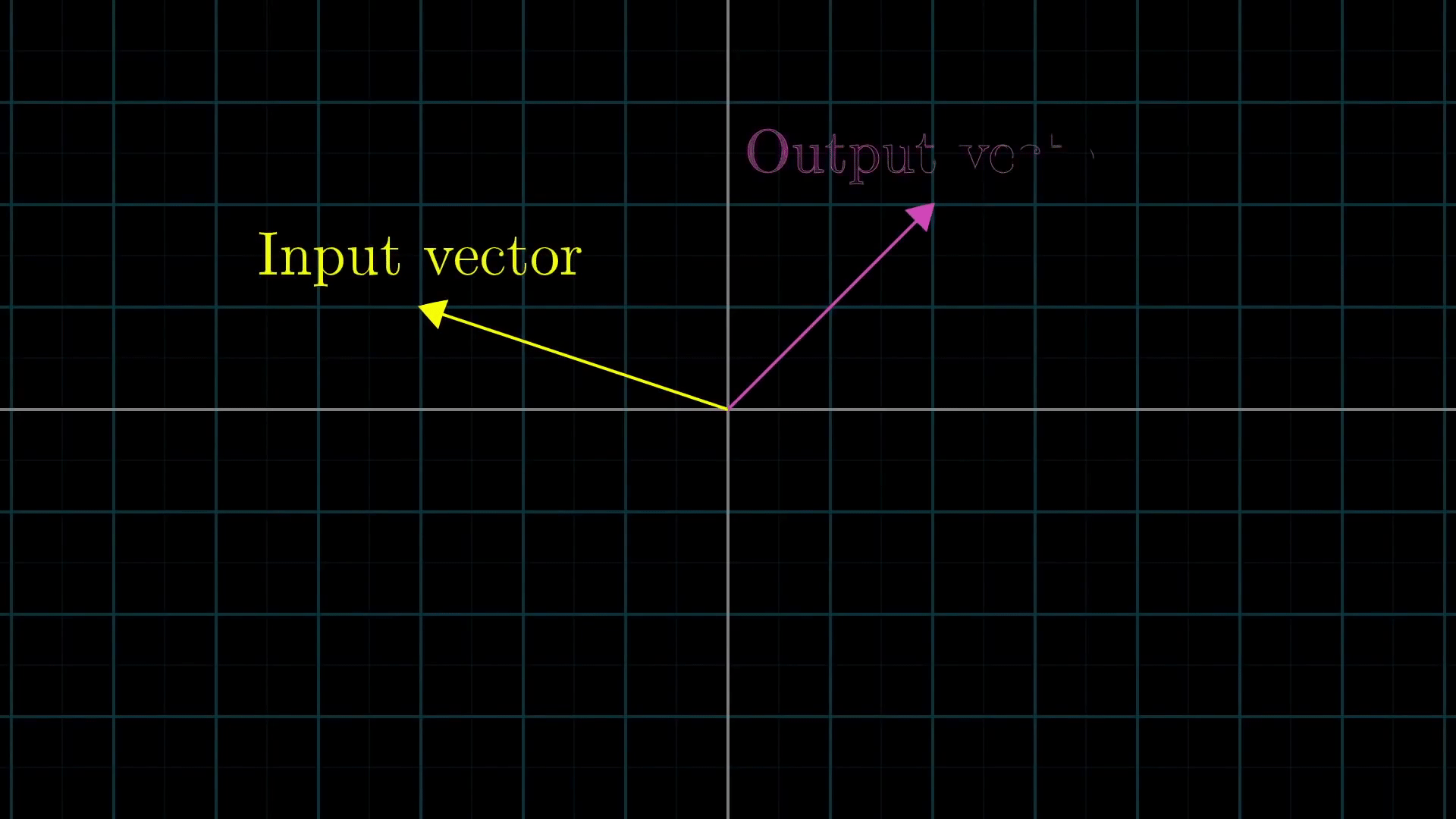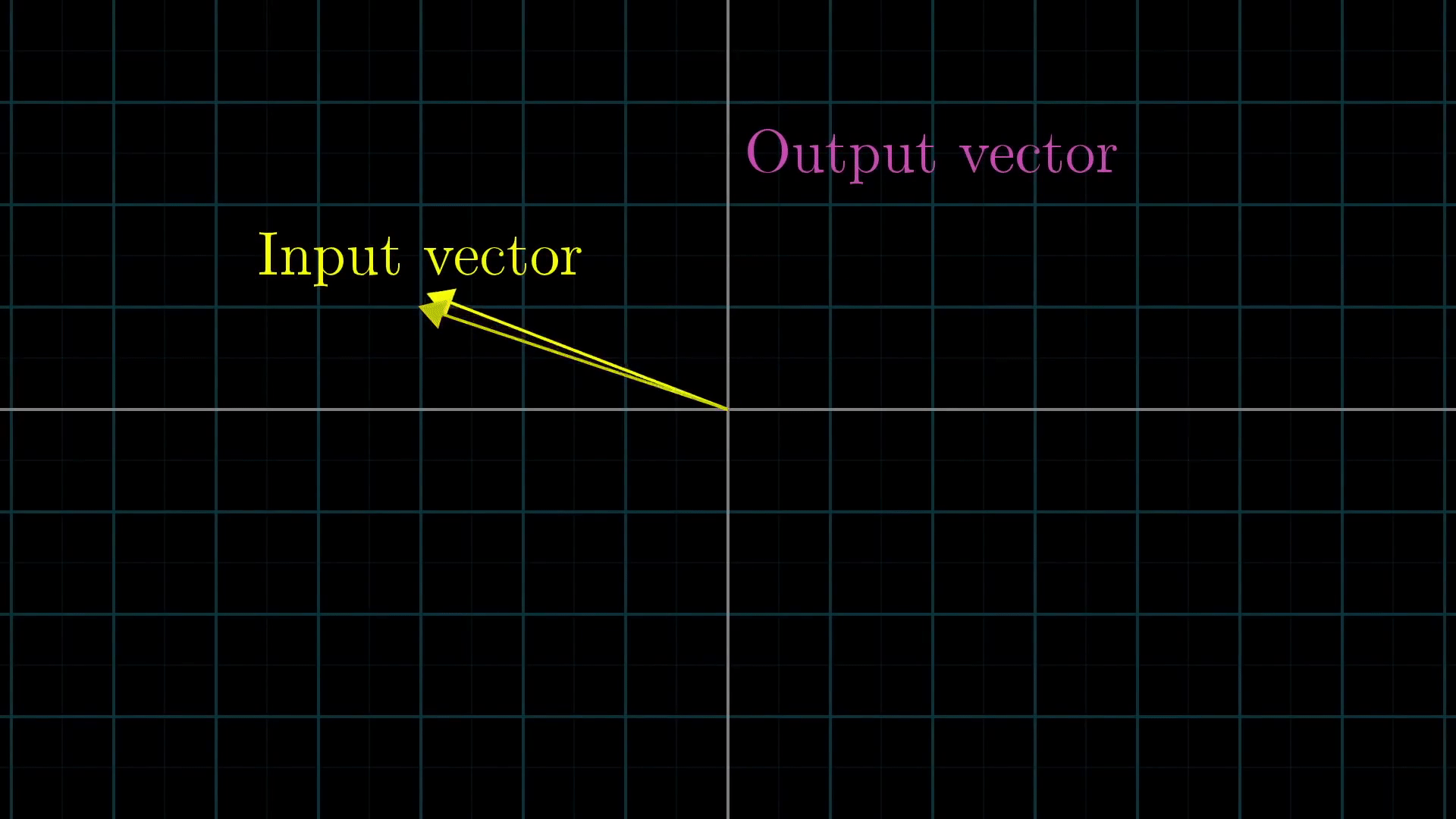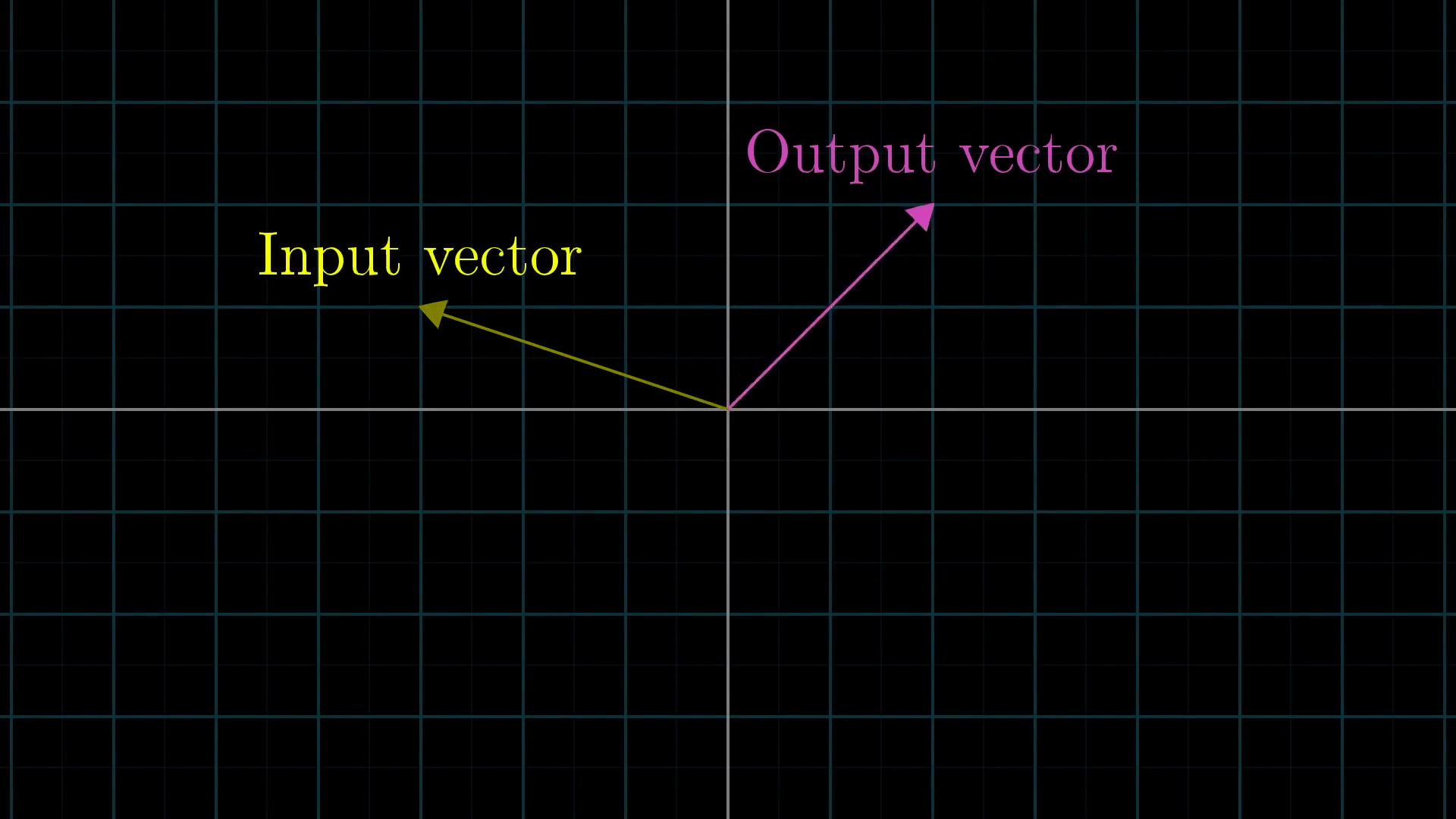
위의 과정은 선형변환을 나타낸다. 어떤 Input vector(노란색 벡터)에 대하여, 그 벡터의 선형변환은 보라색 Output vector가 됨을 확인할 수 있다. 그리고 그 과정에서, 기존의 기저로 표현되어 있던 노란색 벡터는 선형변환된 새로운 기저의 스칼라배(x배,y배)의 합이 된다.
선형변환은 함수와 같아서, 주어진 input 벡터에 대해 변환된 결과인 output 벡터를 return 한다.
이번에는 단일 벡터에서가 아닌 전체적인 scale에서 이 선형변환을 관찰해보자.

벡터는 화살표로 표현하기도 하지만, 일반적으로 벡터가 가리키는 끝 점을 찍어 표현하기도 한다. 위의 GIF는 2차원 평면 좌표 상에서의 점들이 일정하게 선형변환 되는 과정을 보여준다.
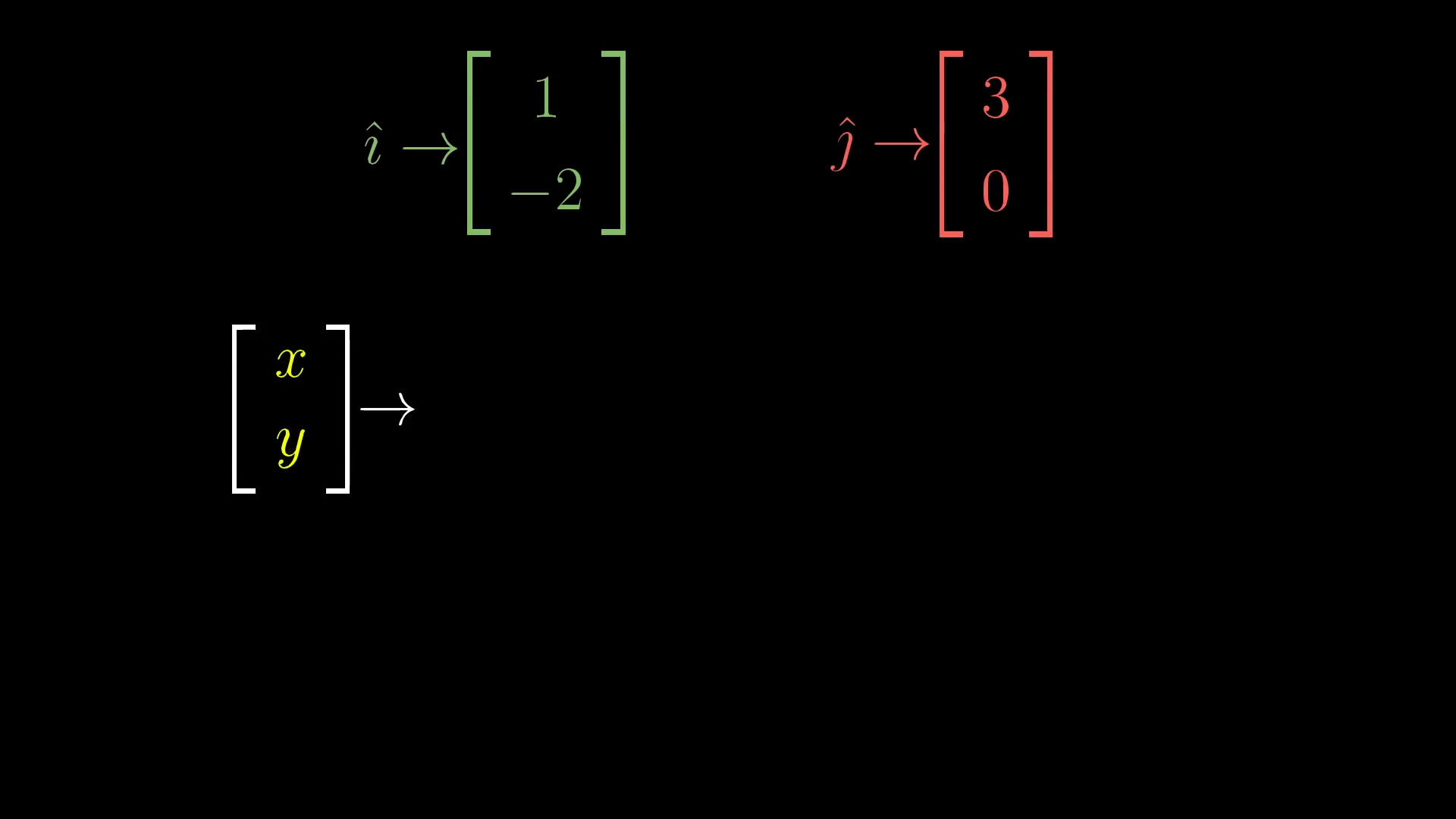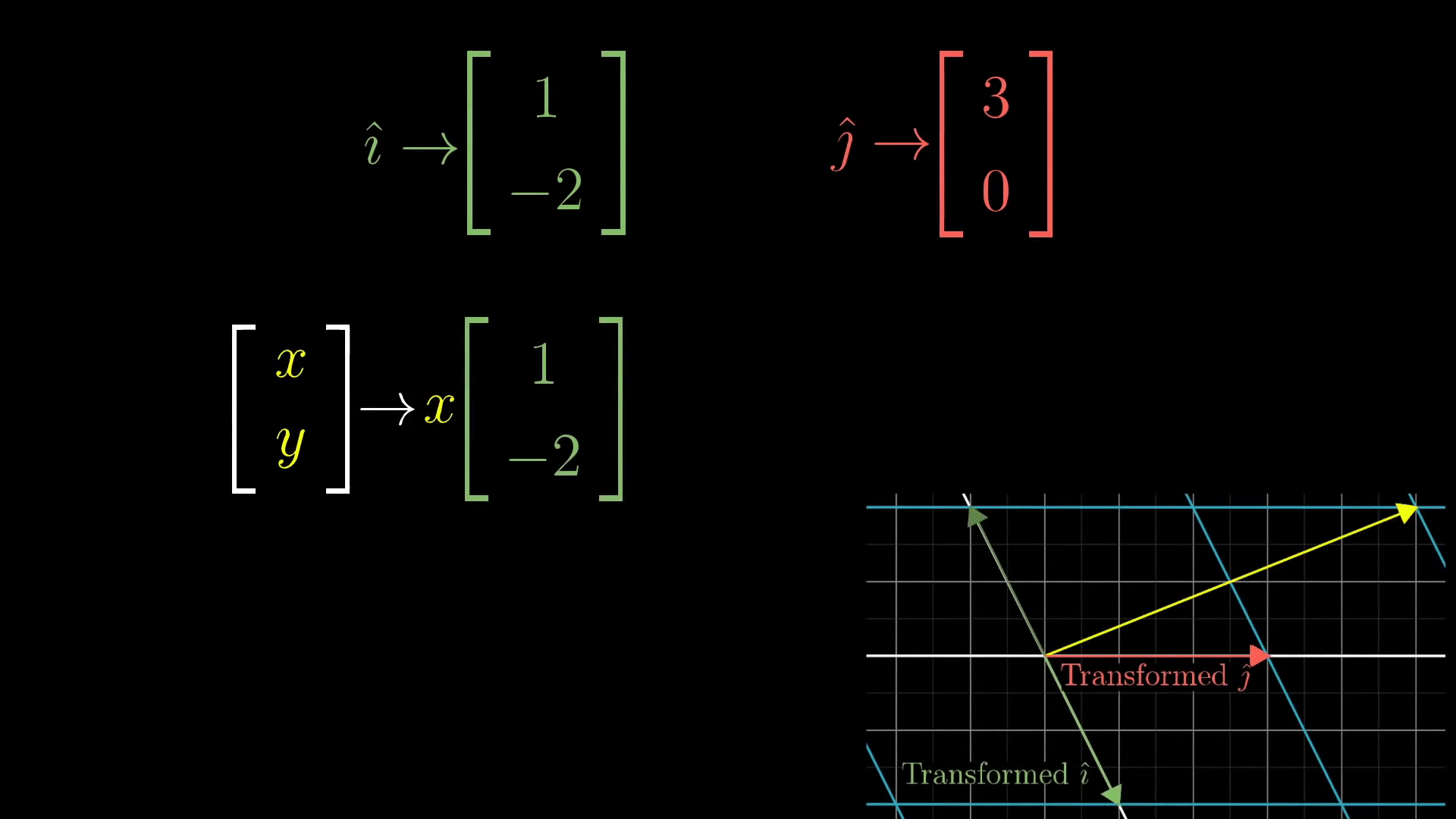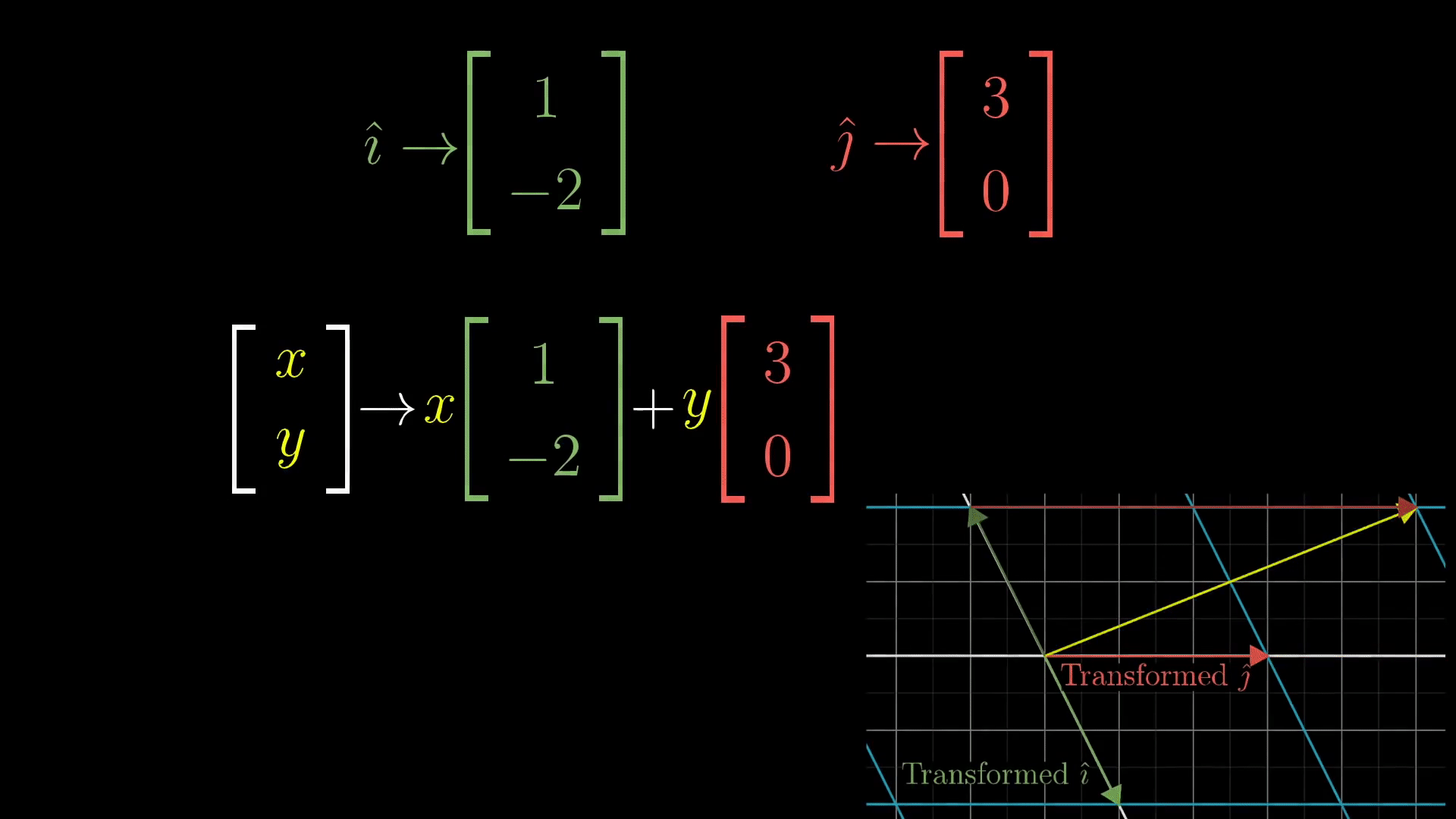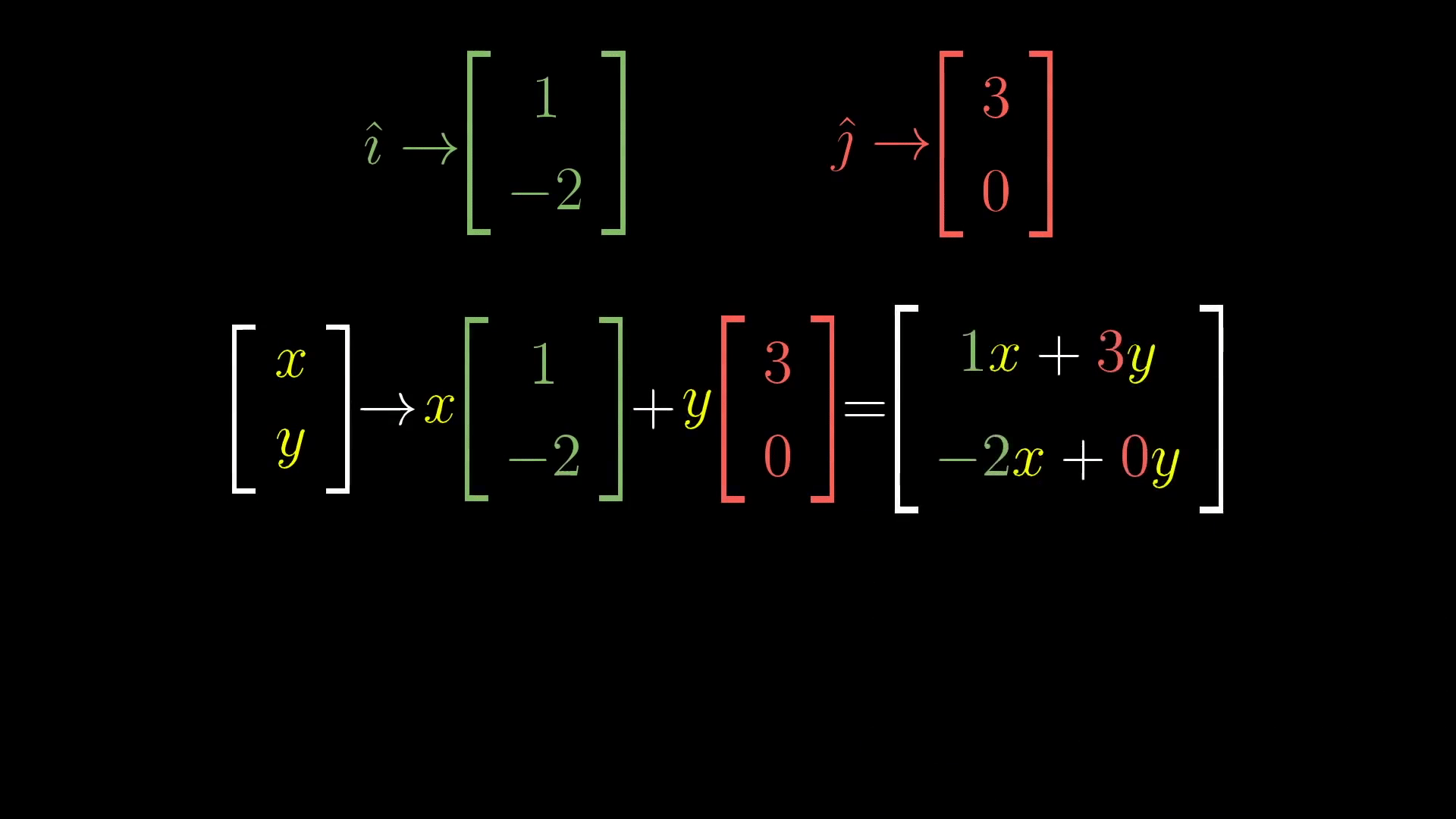
이제 다시 돌아와서 이 선형변환을 '기저의 변환' 이라고 생각하고 위 GIF를 봐보자. 원래의 기저 i와 j가 선형변환에 의해 새로운 기저로 바뀐 후 각각 x배, y배 스칼라 곱이 되어 새로운 벡터를 만들고 있음을 보여준다. 이 선형 변환의 과정에는 오직 [1,-2]^T 벡터와 [3,0]^T 벡터만이 관여 하고 있는 것을 알 수 있는데, 이 두가지의 벡터를 옆을로 붙여 표현하면 2X2 행렬이 된다.
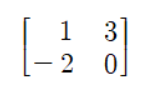
따라서 좀 더 일반적인 상황에서 생각을 해보면 (x,y) 벡터를 선형변환 시키는 행렬과 그 선형변환의 과정은 다음과 같이 나타낼 수 있다.
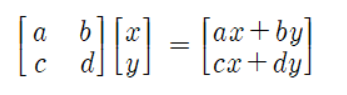
이 때 원래의 기저는 왼쪽 행렬에 의해서 선형변환 되고, 그 후 x배, y배가 더해져 새로운 벡터가 완성된다.
참고로, 선형변환 되었을 때 원점은 유지 되어야 하고, 격자는 휘어져서는 안된다. (선형변환의 정의를 잘 생각 해보면 된다.)
'기초 수학 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 고유값 분해 (0) | 2023.11.19 |
|---|---|
| [선형대수학] 고유값(Eigenvalue)과 고유벡터(Eigenvector) (0) | 2023.11.18 |
| [선형대수학] 역행렬의 의미 (Feat. 행렬식) (1) | 2023.11.18 |
| [선형대수학] 행렬식의 기하학적 의미 (0) | 2023.11.17 |
| [선형대수학] 행렬 곱의 여러가지 해석 (0) | 2023.11.17 |




